
【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.

(1)判断AG与⊙O的位置关系,并说明理由.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
【答案】(1)AG与⊙O相切,证明见解析;(2).
【解析】
试题分析:(1)直线与圆的位置关系有三种,相交,相切,相离,由图形显然AG与⊙O相切,再根据切线的判定定理,运用圆的性质和三角形的等边对等角证明AG垂直于半径OA即可.
(2)求线段OE的长,由题可知△OEF为直角三角形,所以考虑运用勾股定理求解.由圆的性质我们知道△ABC是直角三角形,根据相似三角形的性质可以求出线段EF、BF的长,从而在直角三角形OEF中勾股定理求解.
试题解析:(1)如图 连接OA,∵OA=OB,GA=GE,∴∠ABO=∠BAO,∠GEA=∠GAE.
∵EF⊥BC,∴∠BFE=90°.∴∠ABO+∠BEF=90°.又∵∠BEF=∠GEA,∴∠GAE=∠BEF.
∴∠BAO+∠GAE=90°. ∴OA⊥AG,即AG与⊙O相切.
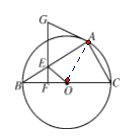
(2)解:∵BC为直径,∴∠BAC=90°.∵AC=6,AB=8,∴BC=10. ∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA.∴==.∴EF=1.8,BF=2.4,
∴OF=OB-BF=5-2.4=2.6. ∴OE==.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列各组线段中是成比例线段的是( )
A. 1㎝,2㎝,3㎝,4㎝ B. 1㎝,2㎝,2㎝,4㎝
C. 3㎝,5㎝,9㎝,13㎝ D. 1㎝,2㎝,2㎝,3㎝
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=2(x﹣1)2+3的顶点坐标是( )
A. (1,3) B. (1,﹣3) C. (﹣1,3) D. (﹣1,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 是半圆
是半圆![]() 的直径,弦
的直径,弦![]() ,动点
,动点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,
,![]() 的延长线与射线
的延长线与射线![]() 相交于点
相交于点![]() 、与弦
、与弦![]() 相交于点
相交于点![]() (点
(点![]() 与点
与点![]() 、
、![]() 不重合),
不重合),![]() ,
,![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围
的取值范围
(3)当![]() 是直角三角形时,求线段
是直角三角形时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
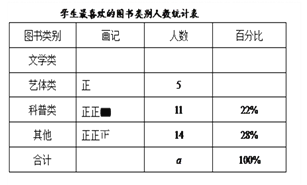
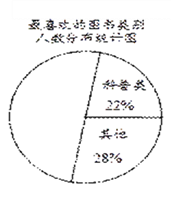

请结合图中的信息解答下列问题:
(1)随机抽取的样本容量a为 ;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
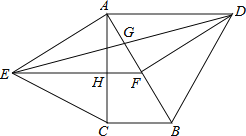
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com