Question

【题目】已知：如图，是半圆的直径，弦，动点、分别在线段、上，且，的延长线与射线相交于点、与弦相交于点（点与点、不重合），，．设，的面积为．

（1）求证：；

（2）求关于的函数关系式，并写出的取值范围

（3）当是直角三角形时，求线段的长．

Answer 1

【答案】（1）证明见解析；（2）（<x<10）.

（3）线段OP的长为8．

【解析】

试题分析：（1）连接OD，通过证明△AOP≌△ODQ后即可证得AP=OQ；

（2）作PH⊥OA，根据cos∠AOC=得到OH=PO=x，从而得到S△AOP=AOPH=3x，利用三角形相似得当对应

边的比相等即可得到函数解析式；

（3）分类讨论：当∠POE=90°时、当∠OPE=90°时、当∠OEP=90°时三种情况讨论即可得到正确的结论.

试题解析：（1）连接OD，在△AOP和△ODQ中，∵OC=OD,∴∠OCD=∠ODC,∵,∴∠OCD=∠COA,∠POA=∠QDO.在△AOP和△ODQ中，

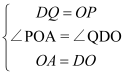，∴△AOP≌△ODQ，∴AP=OQ；

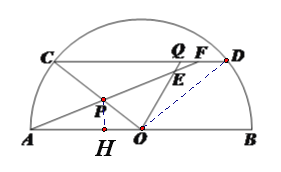
（2）作PH⊥OA交OA于H，∵cos∠AOC=，∴OH= PO= x，PH=x，

∴S△AOP= AOPH=3x，∵,∴△PFC∽△PAO,，

∴,当点F与点D 重合时，∵CD=2OC cos∠OCD=2×10×=16，

解得x=,∴（<x<10）；

（3）当∠POE=90°时，CQ= ，∴PO=DQ=CD﹣CQ= ,∵<x<10,∴PO=（舍）；

当∠OPE=90°时，∠OPA=90°,∴PO=AOcos∠COA=8；

当∠OEP=90°时，∵,∴∠AOQ=∠DQO=∠APO，∴∠AOP=∠AEO=90°,此时弦CD不存在，此种情况不符合题意，舍；

综上，线段OP的长为8．