
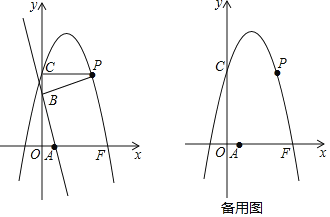
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c与直线y=c分别交y轴的正半轴于点C和第一象限的点P,连接PB,得△PCB≌△BOA(O为坐标原点).若抛物线与x轴正半轴交点为点F,设M是点C,F间抛物线上的一点(包括端点),其横坐标为m.
(1)直接写出点P的坐标和抛物线的解析式;
(2)当m为何值时,△MAB面积S取得最小值和最大值?请说明理由;
(3)求满足∠MPO=∠POA的点M的坐标.
【答案】(1)点P的坐标为(3,4),抛物线的解析式为y=﹣x2+3x+4;(2)当m=0时,S取最小值,最小值为![]() ;当m=3时,S取最大值,最大值为5.(3)满足∠MPO=∠POA的点M的坐标为(0,4)或(
;当m=3时,S取最大值,最大值为5.(3)满足∠MPO=∠POA的点M的坐标为(0,4)或(![]() ,
,![]() ).
).
【解析】(1)代入y=c可求出点C、P的坐标,利用一次函数图象上点的坐标特征可求出点A、B的坐标,再由△PCB≌△BOA即可得出b、c的值,进而可得出点P的坐标及抛物线的解析式;
(2)利用二次函数图象上点的坐标特征求出点F的坐标,过点M作ME∥y轴,交直线AB于点E,由点M的横坐标可得出点M、E的坐标,进而可得出ME的长度,再利用三角形的面积公式可找出S=﹣![]() (m﹣3)2+5,由m的取值范围结合二次函数的性质即可求出S的最大值及最小值;
(m﹣3)2+5,由m的取值范围结合二次函数的性质即可求出S的最大值及最小值;
(3)分两种情况考虑:①当点M在线段OP上方时,由CP∥x轴利用平行线的性质可得出:当点C、M重合时,∠MPO=∠POA,由此可找出点M的坐标;②当点M在线段OP下方时,在x正半轴取点D,连接DP,使得DO=DP,此时∠DPO=∠POA,设点D的坐标为(n,0),则DO=n,DP=![]() ,由DO=DP可求出n的值,进而可得出点D的坐标,由点P、D的坐标利用待定系数法即可求出直线PD的解析式,再联立直线PD及抛物线的解析式成方程组,通过解方程组求出点M的坐标.综上此题得解.
,由DO=DP可求出n的值,进而可得出点D的坐标,由点P、D的坐标利用待定系数法即可求出直线PD的解析式,再联立直线PD及抛物线的解析式成方程组,通过解方程组求出点M的坐标.综上此题得解.
(1)当y=c时,有c=﹣x2+bx+c,
解得:x1=0,x2=b,
∴点C的坐标为(0,c),点P的坐标为(b,c),
∵直线y=﹣3x+3与x轴、y轴分别交于A、B两点,
∴点A的坐标为(1,0),点B的坐标为(0,3),
∴OB=3,OA=1,BC=c﹣3,CP=b,
∵△PCB≌△BOA,
∴BC=OA,CP=OB,
∴b=3,c=4,
∴点P的坐标为(3,4),抛物线的解析式为y=﹣x2+3x+4;
(2)当y=0时,有﹣x2+3x+4=0,
解得:x1=﹣1,x2=4,
∴点F的坐标为(4,0),
过点M作ME∥y轴,交直线AB于点E,如图1所示,
∵点M的横坐标为m(0≤m≤4),
∴点M的坐标为(m,﹣m2+3m+4),点E的坐标为(m,﹣3m+3),
∴ME=﹣m2+3m+4﹣(﹣3m+3)=﹣m2+6m+1,
∴S=![]() OAME=﹣
OAME=﹣![]() m2+3m+
m2+3m+![]() =﹣
=﹣![]() (m﹣3)2+5,
(m﹣3)2+5,
∵﹣![]() <0,0≤m≤4,
<0,0≤m≤4,
∴当m=0时,S取最小值,最小值为![]() ;当m=3时,S取最大值,最大值为5;
;当m=3时,S取最大值,最大值为5;
(3)①当点M在线段OP上方时,∵CP∥x轴,
∴当点C、M重合时,∠MPO=∠POA,
∴点M的坐标为(0,4);
②当点M在线段OP下方时,在x正半轴取点D,连接DP,使得DO=DP,此时∠DPO=∠POA,
设点![]() ,
,
∴n2=(n﹣3)2+16,
解得:n=![]() ,
,
∴点D的坐标为(![]() ,0),
,0),
设直线PD的解析式为y=kx+a(k≠0),
将P(3,4)、D(![]() ,0)代入y=kx+a,
,0)代入y=kx+a,
 ,解得:
,解得: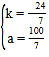 ,
,
∴直线PD的解析式为y=﹣![]() x+
x+![]() ,
,
联立直线PD及抛物线的解析式成方程组,得: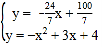 ,
,
解得:![]() ,
,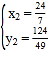 .
.
∴点M的坐标为(![]() ,
,![]() ).
).
综上所述:满足∠MPO=∠POA的点M的坐标为(0,4)或(![]() ,
,![]() ).
).

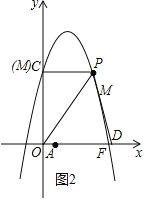


科目:初中数学 来源: 题型:
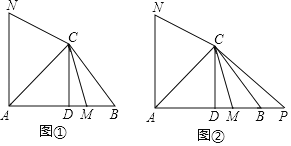
【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:![]() ;
;
(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
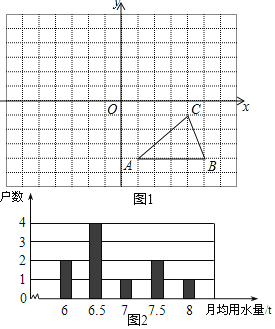
(1)如图1,方格纸中的每个小方格都是边长为1个单位长的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①作出△ABC关于x轴对称的△A1B1C1;
②如果P点的纵坐标为3,且P点到直线AA的距离为5,请直接写出点P的坐标.
(2)我国是世界上严重缺水的国家之一为了倡导“节约用水,从我做起”,小丽同学在她家所在小区的200住户中,随机调查了10个家庭在2019年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图2
①求这10个样本数据的平均数;
②以上面的样本平均数为依据,自来水公司按2019年该小区户月均用水量下达了2020年的用水计划(超计划要执行阶梯式标准收费)请计算该小区2020年的计划用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
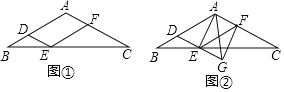
【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境观察:
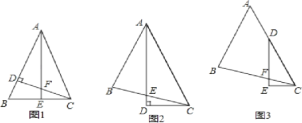
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知卖出的糖果数量x(kg)与售价y(元)的关系如下表:
数量x(kg) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 |
(1)这个表格反映了哪两个变量之间的关系?它们的关系式是什么?
(2)若某顾客付了14.7元,则他购买了多少千克的糖果?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划成立下列学生社团: A.合唱团: B.英语俱乐部: C.动漫创作社; D.文学社:E.航模工作室为了解同学们对上述学生社团的喜爱情况某课题小组在全校学生中随机抽取了部分同学,进行“你最喜爱的一个学生社团”的调查,根据调查结果绘制了如下尚不完整的统计图.
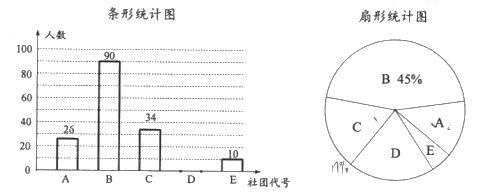
请根据以上信息,解决下列问题:
(1)本次接受调查的学生共有多少人;
(2)补全条形统计图,扇形统计图中D选项所对应扇形的圆心角为多少;
(3)若该学校共有学生3000人,估计该学校学生中喜爱合唱团和动漫创作社的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com