
【题目】“安全教育”是学校必须开展的一项重要工作.某校为了了解家长和学生参与“暑期安全知识学习”的情况,进行了网上测试,并在本校学生中随机抽取部分学生进行调查.若把参与测试的情况分为![]() 类情形:
类情形:![]() .仅学生自己参与;
.仅学生自己参与;![]() .家长和学生一起参与;
.家长和学生一起参与;![]() .仅家长自己参与;
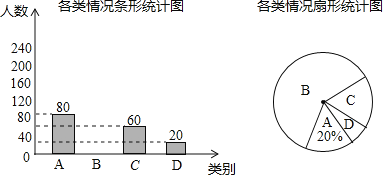
.仅家长自己参与;![]() .家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
.家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
![]() 在这次抽样调查中,共调查了 名学生;
在这次抽样调查中,共调查了 名学生;
![]() 补全条形统计图,并计算扇形统计图中
补全条形统计图,并计算扇形统计图中![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
![]() 根据抽样调查结果,估计该校
根据抽样调查结果,估计该校![]() 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
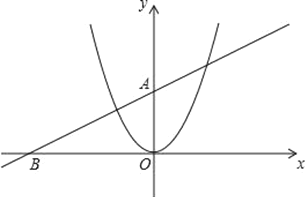
【题目】已知直线y=kx+b经过点A(0,2),B(﹣4,0)和抛物线y=x2.
(1)求直线的解析式;
(2)将抛物线y=x2沿着x轴向右平移,平移后的抛物线对称轴左侧部分与y轴交于点C,对称轴右侧部分抛物线与直线y=kx+b交于点D,连接CD,当CD∥x轴时,求平移后得到的抛物线的解析式;
(3)在(2)的条件下,平移后得到的抛物线的对称轴与x轴交于点E,P为该抛物线上一动点,过点P作抛物线对称轴的垂线,垂足为Q,是否存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
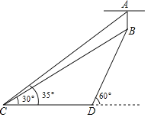
【题目】如图,宾馆大厅的天花板上挂有一盏吊灯AB,某人从C点测得吊灯顶端A的仰角为![]() ,吊灯底端B的仰角为
,吊灯底端B的仰角为![]() ,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为
,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为![]() .请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,
.请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
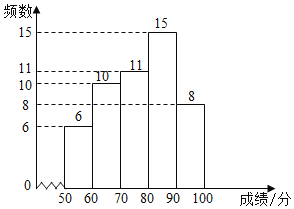
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 轴于点
轴于点![]() ,且
,且![]() .
.
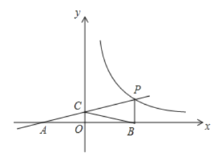
(1)求一次函数、反比例函数的解析式;
(2)根据图像直接写出![]() 的
的![]() 的取值范围;
的取值范围;
(3)点![]() 为反比例函数图象上使得四边形
为反比例函数图象上使得四边形![]() 为菱形的一点,点
为菱形的一点,点![]() 为
为![]() 轴上的一动点,当
轴上的一动点,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:
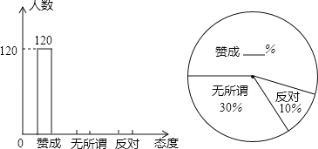
根据上述信息,解答下列问题:
(1)抽取的学生人数为 ;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
上课时孙老师提出这样一个问题:对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
小明的思路是:原不等式等价于![]() ,设函数
,设函数![]() ,
,![]() ,画出两个函数的图象的示意图,于是原问题转化为函数
,画出两个函数的图象的示意图,于是原问题转化为函数![]() 的图象在
的图象在![]() 的图象上方时
的图象上方时![]() 的取值范围.
的取值范围.

请结合小明的思路回答:
对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是_____.
的取值范围是_____.
参考小明思考问题的方法,解决问题:
关于![]() 的方程
的方程![]() 在
在![]() 范围内有两个解,求
范围内有两个解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com