
【题目】如图,边长为4的等边三角形AOB的顶点O在坐标原点,点A在x轴的正半轴上,点B在第一象限.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.过点P作PD⊥OB于D点
(1)直接写出BD的长并求出点C的坐标(用含t的代数式表示)
(2)在点P从O向A运动的过程中,△PCA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(3)点P从点O运动到点A时,点C运动路线的长是多少?
【答案】
(1)解:∵△AOB是等边三角形,
∴OB=OA=AB=4,∠BOA=∠OAB=∠ABO=60°.
∵PD⊥OB,
∴∠PDO=90°,
∴∠OPD=30°,
∴OD= ![]() OP.
OP.
∵OP=t,
∴OD= ![]() t,
t,
∴BD=4﹣ ![]() t.
t.
在Rt△OPD中,由勾股定理,得PD= ![]() t,
t,
如图(1),过C作CE⊥OA于E,

则∠PEC=90°,
∵线段BP的中点绕点P按顺时针方向旋转60°得点C,
∴∠BPC=60°.
∵∠OPD=30°,
∴∠BPD+∠CPE=90°.
∴∠DBP=∠CPE
∴△PCE∽△BPD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴CE= ![]() ,PE=2﹣
,PE=2﹣ ![]() ,
,
∴OE=OP+PE=2+ ![]() ,
,
∴C(2+ ![]() ,
, ![]() )
)
(2)解:如图(3),当∠PCA=90度时,作CF⊥PA,

∴△PCF∽△ACF,
∴ ![]() =
= ![]() ,
,
∴CF2=PFAF,
∵PF=2﹣ ![]() t,AF=4﹣OF=2﹣
t,AF=4﹣OF=2﹣ ![]() t,CF=
t,CF= ![]() t,
t,
∴( ![]() t)2=(2﹣
t)2=(2﹣ ![]() t)(2﹣
t)(2﹣ ![]() t),
t),
解得t=2,
此时P是OA的中点.
如图(2),

当∠CAP=90°时,C的横坐标就是4,
∴2+ ![]() t=4,
t=4,
解得t= ![]()
(3)解:设C(x,y),
∴x=2+ ![]() t,y=
t,y= ![]() t,
t,
∴y= ![]() x﹣
x﹣ ![]() ,
,
∴C点的运动痕迹是一条线段(0≤t≤4).
当t=0时,C1(2,0),
当t=4时,C2(5, ![]() ),
),
∴由两点间的距离公式得:C1C2=2 ![]() .
.
故点C运动路线的长为:2 ![]()
【解析】(1)利用30度角的性质和旋转性质、相似三角形性质,即△PCE∽△BPD,对应边成比例可求出C坐标;(2)可先假设△PCA能成为直角三角形,分类讨论,当∠PCA=90度时或∠CAP=90°,可利用相似性质列出对应边成比例式子,进行求解;(3)可设出设C(x,y),构建参数方程x=2+ ![]() t,y=
t,y= ![]() t,消去参数即可得到y=
t,消去参数即可得到y= ![]() x﹣
x﹣ ![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AB∥OC,A(0,﹣4),B(a,b),C(c,0),并且a,c满足c=![]() +10.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P,Q分别从点A,O同时出发,当点P运动到点B时,点Q随之停止运动,设运动时间为t(秒).
+10.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P,Q分别从点A,O同时出发,当点P运动到点B时,点Q随之停止运动,设运动时间为t(秒).
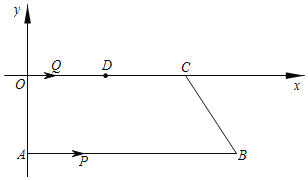
(1)求B,C两点的坐标;
(2)当t为何值时,四边形PQCB是平行四边形?
(3)点D为线段OC的中点,当t为何值时,△OPD是等腰三角形?直接写出t的所有值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点O为对角线AC的中点,过点o作射线OG、ON分别交AB,BC于点E,F,且∠EOF=90°,BO、EF交于点P.则下列结论中:
⑴图形中全等的三角形只有两对;
⑵正方形ABCD的面积等于四边形OEBF面积的4倍;
⑶BE+BF= ![]() OA;
OA;
⑷AE2+CF2=2OPOB.
正确的结论有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲船匀速顺流而下从![]() 港到
港到![]() 港,同时乙船匀速逆流而上从
港,同时乙船匀速逆流而上从![]() 港到
港到![]() 港,
港,![]() 港处于
港处于![]() 、
、![]() 两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到
两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到![]() 处,到
处,到![]() 处后迅速按原顺流速度驶向
处后迅速按原顺流速度驶向![]() 港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与
港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与![]() 港的距离之和为
港的距离之和为![]() ,行驶时间为
,行驶时间为![]() ,
,![]() 与
与![]() 的部分关系如图,则当两船在
的部分关系如图,则当两船在![]() 、
、![]() 间某处相超时,两船距离
间某处相超时,两船距离![]() 港的距离为________千米.
港的距离为________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为_____.
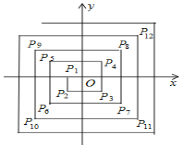
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为( )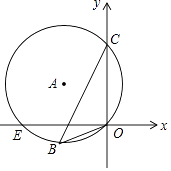
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“湘一四边形”.
(1)已知:如图1,四边形![]() 是“湘一四边形”,
是“湘一四边形”,![]() ,
,![]() ,
,![]() .则
.则![]() ,
, ![]() ,若
,若![]() ,
,![]() ,则
,则![]() (直接写答案)
(直接写答案)
(2)已知:在“湘一四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .求对角线
.求对角线![]() 的长(请画图求解),
的长(请画图求解),
(3)如图(2)所示,在四边形![]() 中,若
中,若![]() ,当
,当![]() 时,此时四边形
时,此时四边形![]() 是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
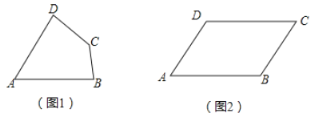
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市荸荠喜获丰收,某生产基地收获荸荠40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润(百元/吨) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com