
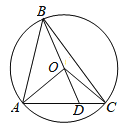
【题目】如图,已知![]() 的半径为1,
的半径为1,![]() ,
,![]() 是
是![]() 的两条弦,且
的两条弦,且![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,则
,则![]() =__________.
=__________.
【答案】![]()
【解析】
可证△AOB≌△AOC,推出∠ACO=∠ABD,OA=OC,∠OAC=∠ACO=∠ABD,∠ADO=∠ADB,即可证明△OAD∽△ABD;依据对应边成比例,设OD=x,表示出AB、AD,根据AD2=ABDC,列方程求解即可.
解:在△AOB和△AOC中,
∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠ABO=∠ACO,
∵OA=OC,
∴∠ACO=∠OAD,
∵∠ADO=∠BDA,
∴△ADO∽△BDA,
∴![]() ,
,
设OD=x,则BD=1+x,
∴![]() ,
,
∴AD=![]() ,AB=
,AB=![]() ,
,
∵DC=AC-AD=AB-AD,AD2=ABDC,
(![]() )2═
)2═![]() (
(![]() -
-![]() ),
),
整理得:x2+x-1=0,
解得:x=![]() 或x=
或x=![]() (舍去),
(舍去),
因此OD=![]() ,
,
故答案为:![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过三点(1,0),(-6,0)(0,-3).
的图象经过三点(1,0),(-6,0)(0,-3).
(1)求该二次函数的解析式.
(2)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象在第一象限内交于点A(
的图象在第一象限内交于点A(![]() ),
),![]() 落在两个相邻的正整数之间,请求出这两个相邻的正整数.
落在两个相邻的正整数之间,请求出这两个相邻的正整数.
(3)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象在第一象限内的交点为B,点B的横坐标为m,且满足3<m<4,求实数k的取值范围.
的图象在第一象限内的交点为B,点B的横坐标为m,且满足3<m<4,求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,线段PD最长?并求出最大值;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,求点M的坐标.(请直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
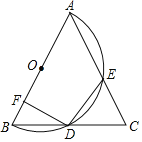
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,交AC于点E.
(1)求证:BD=CD.
(2)若弧DE=50°,求∠C的度数.
(3)过点D作DF⊥AB于点F,若BC=8,AF=3BF,求弧BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论:①a﹣b+c<0;②2a+b+c>0;③x(αx+b)≤a+b;④a>﹣1.其中正确的有( )
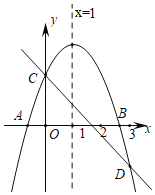
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.
(1)当吊臂底部A与货物的水平距离AC为5m时,求吊臂AB的长;
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计,计算结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC .

(1)若∠DFC=40,求∠CBF的度数.
(2)求证: CD⊥DF .
查看答案和解析>>
科目:初中数学 来源: 题型:
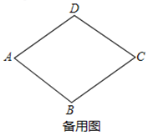
【题目】如图1,在菱形![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 边以每秒1个单位长度的速度运动到点
边以每秒1个单位长度的速度运动到点![]() 时停止,连接
时停止,连接![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).

(1)菱形![]() 对角线
对角线![]() 的长为 ;
的长为 ;
(2)当点![]() 恰在
恰在![]() 上时,求t的值;
上时,求t的值;
(3)当![]() 时,求
时,求![]() 的周长;
的周长;
(4)直接写出在整个运动过程中,点![]() 运动的路径长.
运动的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com