
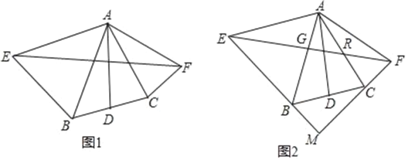
【题目】已知,如图AD为△ABC的中线,分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF,且AE=AB,AF=AC,连接EF,∠EAF+∠BAC=180°
(1)如图1,若∠ABE=63°,∠BAC=45°,求∠FAC的度数;
(2)如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;
(3)如图2,设EF交AB于点G,交AC于点R,延长FC,EB交于点M,若点G为线段EF的中点,且∠BAE=70°,请探究∠ACB和∠CAF的数量关系,并证明你的结论.
【答案】(1)36°;(2)EF=2AD,见解析;(3)![]() ,见解析.
,见解析.
【解析】
(1)由等腰三角形的性质得出∠AEB=∠ABE=63°,由三角形内角和定理得出∠EAB=54°,推出∠EAB+2∠BAC+∠FAC=180°,即可得出结果;
(2)延长AD至H,使DH=AD,连接BH,由中线的性质得出BD=CD,由SAS证得△BDH≌△CDA得出HB=AC=AF,∠BHD=∠CAD,得出AC∥BH,由平行线的性质得出∠ABH+∠BAC=180°,证得∠EAF=∠ABH,由SAS证得△ABH≌△EAF,即可得出结论;
(3)由(2)得,AD=![]() EF,又点G为EF中点,得出EG=AD,由(2)△ABH≌△EAF得出∠AEG=∠BAD,由SAS证得△EAG≌△ABD得出∠EAG=∠ABC=70°,由已知得出∠EAB+2∠BAC+∠CAF=180°,推出∠BAC=55°-
EF,又点G为EF中点,得出EG=AD,由(2)△ABH≌△EAF得出∠AEG=∠BAD,由SAS证得△EAG≌△ABD得出∠EAG=∠ABC=70°,由已知得出∠EAB+2∠BAC+∠CAF=180°,推出∠BAC=55°-![]() ∠CAF,由三角形内角和定理得出∠BAC=180°-∠ABC-∠ACB=110°-∠ACB,即可得出结果.
∠CAF,由三角形内角和定理得出∠BAC=180°-∠ABC-∠ACB=110°-∠ACB,即可得出结果.
(1)∵AE=AB,
∴∠AEB=∠ABE=63°,
∴∠EAB=54°,
∵∠BAC=45°,∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠FAC=180°,
∴54°+2×45°+∠FAC=180°,
∴∠FAC=36°;
(2)EF=2AD;理由如下:
延长AD至H,使DH=AD,连接BH,如图1所示:
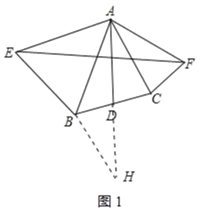
∵AD为△ABC的中线,
∴BD=CD,
在△BDH和△CDA中,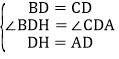 ,
,
∴△BDH≌△CDA(SAS),
∴HB=AC=AF,∠BHD=∠CAD,
∴AC∥BH,
∴∠ABH+∠BAC=180°,
∵∠EAF+∠BAC=180°,
∴∠EAF=∠ABH,
在△ABH和△EAF中,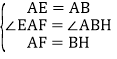 ,
,
∴△ABH≌△EAF(SAS),
∴EF=AH=2AD;
(3)![]() ;理由如下:
;理由如下:
由(2)得,AD=![]() EF,又点G为EF中点,
EF,又点G为EF中点,
∴EG=AD,
由(2)△ABH≌△EAF,
∴∠AEG=∠BAD,
在△EAG和△ABD中,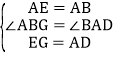 ,
,
∴△EAG≌△ABD(SAS),
∴∠EAG=∠ABC=70°,
∵∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠CAF=180°,
即:70°+2∠BAC+∠CAF=180°,
∴∠BAC+![]() ∠CAF=55°,
∠CAF=55°,
∴∠BAC=55°﹣![]() ∠CAF,
∠CAF,
∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣∠ACB=110°﹣∠ACB,
∴55°﹣![]() ∠CAF=110°﹣∠ACB,
∠CAF=110°﹣∠ACB,
∴∠ACB﹣![]() ∠CAF=55°.
∠CAF=55°.


科目:初中数学 来源: 题型:
【题目】填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.

证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间福州一中初中部举行了“宅家运动会”.该学校七、八年级各有300名学生参加了这次“宅家运动会”,现从七、八年级各随机抽取20名学生宅家运动会的成绩进行抽样调查.
收集数据如下:
七年级: | 74 | 97 | 96 | 72 | 98 | 99 | 72 | 73 | 76 | 74 |
74 | 69 | 76 | 89 | 78 | 74 | 99 | 97 | 98 | 99 | |
八年级: | 76 | 88 | 96 | 89 | 78 | 94 | 89 | 94 | 95 | 50 |
89 | 68 | 65 | 89 | 77 | 86 | 89 | 88 | 92 | 91 |
整理数据如下:
|
|
|
|
| |
七年级 | 0 | 1 | 10 | 1 | a |
八年级 | 1 | 2 | 3 | 8 | 6 |
分析数据如下:
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 84.2 | 77 | 74 | 138.56 |
八年级 | 84 | b | 89 | 129.7 |
根据以上信息,回答下列问题:
(1)![]() ___________,
___________,![]() ___________;
___________;
(2)你认为哪个年级“宅家运动会”的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性)
(3)学校对“宅家运动会”成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有___________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
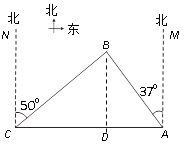
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
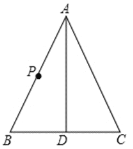
【题目】如图,在△ABC中,AB=AC, AD是△ABC 底边BC上的中线,P为AB上一点.
(1)在AD上找一点E,使得PE+EB的值最小;
(2)若P为AB的中点,当∠BPE= °时,△ABC是等边三角形.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界上大部分国家都使用摄氏温度(![]() ),但美国、英国等国家的天气预报仍然使用华氏温度(
),但美国、英国等国家的天气预报仍然使用华氏温度(![]() ).两种计量之间有如下对应:
).两种计量之间有如下对应:
摄氏温度( |
|
|
|
|
|
|
华氏温度( |
|
|
|
|
|
|
(1)上表反映了哪两变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(![]() )每提高
)每提高![]() 度,华氏温度(
度,华氏温度(![]() )提高_____度.
)提高_____度.
(3)摄氏温度![]() 度时华氏温度为______度.
度时华氏温度为______度.
(4)华氏温度![]() 度时摄氏温度为_______度.
度时摄氏温度为_______度.
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二孩子政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度,在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:
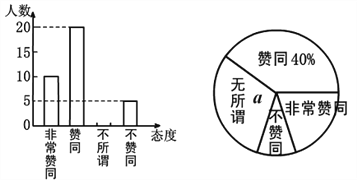
(1)在这次问卷调查中一共抽取了__________名学生,a=________%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com