一张桌子上摆放有若干个大小、形状完全相同的碟子，现从三个方向看，其三种视图如图所示，则这张桌子上碟子的总数为（ ）
|
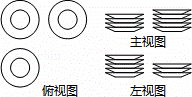
| A． | 11 | B． | 12 | C． | 13 | D． | 14 |
科目：初中数学 来源： 题型：
在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（ ）
|
| A． | （4，﹣3） | B． | （﹣4，3） | C． | （0，﹣3） | D． | （0，3） |
查看答案和解析>>
科目：初中数学 来源： 题型：
已知双曲线y=
（x＞0），直线l1：y﹣
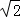=k（x﹣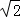）（k＜0）过定点F且与双曲线交于A，B两点，设A（x1，y1），B（x2，y2）（x1＜x2），直线l2：y=﹣x+．
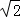（1）若k=﹣1，求△OAB的面积S；
（2）若AB=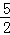
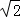，求k的值；
（3）设N（0，2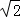），P在双曲线上，M在直线l2上且PM∥x轴，求PM+PN最小值，并求PM+PN取得最小值时P的坐标．（参考公式：在平面直角坐标系中，若A（x1，y1），B（x2，y2）则A，B两点间的距离为AB=
）
查看答案和解析>>
科目：初中数学 来源： 题型：
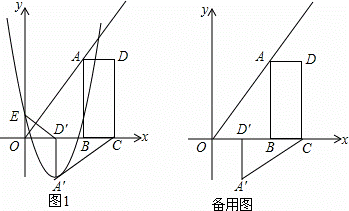
如图1，B（2m，0），C（3m，0）是平面直角坐标系中两点，其中m为常数，且m＞0，E（0，n）为y轴上一动点，以BC为边在x轴上方作矩形ABCD，使AB=2BC，画射线OA，把△ADC绕点C逆时针旋转90°得△A′D′C′，连接ED′，抛物线y=ax2+bx+n（a≠0）过E，A′两点．
（1）填空：∠AOB= 45 °，用m表示点A′的坐标：A′（ m ， ﹣m ）；
（2）当抛物线的顶点为A′，抛物线与线段AB交于点P，且
=
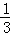时，△D′OE与△ABC是否相似？说明理由；
（3）若E与原点O重合，抛物线与射线OA的另一个交点为点M，过M作MN⊥y轴，垂足为N：
①求a，b，m满足的关系式；
②当m为定值，抛物线与四边形ABCD有公共点，线段MN的最大值为10，请你探究a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x，下列式子中错误的是（ ）
|
| A． | [x]=x（x为整数） | B． | 0≤x﹣[x]＜1 |
|
| C． | [x+y]≤[x]+[y] | D． | [n+x]=n+[x]（n为整数） |
查看答案和解析>>
科目：初中数学 来源： 题型：
在等腰△ABC中，AB=AC，则有BC边上的中线，高线和∠BAC的平分线重合于AD（如图一）．若将等腰△ABC的顶点A向右平行移动后，得到△A′BC（如图二），那么，此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 ， ， ．（填A′D、A′E、A′F）
查看答案和解析>>
科目：初中数学 来源： 题型：
某中学要在全校学生中举办“中国梦•我的梦”主题演讲比赛，要求每班选一名代表参赛．九年级（1）班经过投票初选，小亮和小丽票数并列班级第一，现在他们都想代表本班参赛．经班长与他们协商决定，用他们学过的掷骰子游戏来确定谁去参赛（胜者参赛）．
规则如下：两人同时随机各掷一枚完全相同且质地均匀的骰子一次，向上一面的点数都是奇数，则小亮胜；向上一面的点数都是偶数，则小丽胜；否则，视为平局，若为平局，继续上述游戏，直至分出胜负为止．
如果小亮和小丽按上述规则各掷一次骰子，那么请你解答下列问题：
（1）小亮掷得向上一面的点数为奇数的概率是多少？
（2）该游戏是否公平？请用列表或树状图等方法说明理由．（骰子：六个面上分别刻有1，2，3，4，5，6个小圆点的小正方体）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
+
．