
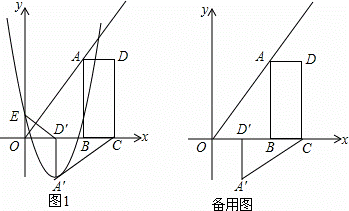
如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E,A′两点.
(1)填空:∠AOB= 45 °,用m表示点A′的坐标:A′( m , ﹣m );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且 =
=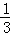 时,△D′OE与△ABC是否相似?说明理由;
时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
解:(1)∵B(2m,0),C(3m,0),
∴OB=2m,OC=3m,即BC=m,
∵AB=2BC,
∴AB=2m=0B,
∵∠ABO=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,
由旋转的性质得:OD′=D′A′=m,即A′(m,﹣m);
故答案为:45;m,﹣m;
(2)△D′OE∽△ABC,理由如下:
由已知得:A(2m,2m),B(2m,0),
∵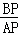 =
=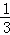 ,
,
∴P(2m,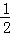 m),
m),
∵A′为抛物线的顶点,
∴设抛物线解析式为y=a(x﹣m)2﹣m,
∵抛物线过点E(0,n),
∴n=a(0﹣m)2﹣m,即m=2n,
∴OE:OD′=BC:AB=1:2,
∵∠EOD′=∠ABC=90°,
∴△D′OE∽△ABC;
(3)①当点E与点O重合时,E(0,0),
∵抛物线y=ax2+bx+c过点E,A,
∴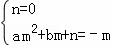 ,
,
整理得:am+b=﹣1,即b=﹣1﹣am;
②∵抛物线与四边形ABCD有公共点,
∴抛物线过点C时的开口最大,过点A时的开口最小,
若抛物线过点C(3m,0),此时MN的最大值为10,
∴a(3m)2﹣(1+am)•3m=0,
整理得:am=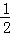 ,即抛物线解析式为y=
,即抛物线解析式为y=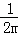 x2﹣
x2﹣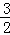 x,
x,
由A(2m,2m),可得直线OA解析式为y=x,
联立抛物线与直线OA解析式得: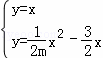 ,
,
解得:x=5m,y=5m,即M(5m,5m),
令5m=10,即m=2,
当m=2时,a=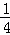 ;
;
若抛物线过点A(2m,2m),则a(2m)2﹣(1+am)•2m=2m,
解得:am=2,
∵m=2,
∴a=1,
则抛物线与四边形ABCD有公共点时a的范围为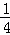 ≤a≤1
≤a≤1


科目:初中数学 来源: 题型:
下列说法正确的是( )
|
| A. | “购买1张彩票就中奖”是不可能事件 |
|
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 |
|
| C. | 了解我国青年人喜欢的电视节目应作全面调查 |
|
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
查看答案和解析>>
科目:初中数学 来源: 题型:
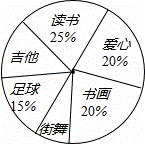
901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
(1)该班的学生共有 60 名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
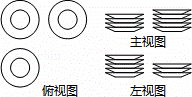
|
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
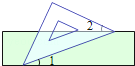
|
| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com