科目：初中数学 来源： 题型：
如图1，一条抛物线与
轴交于A，B两点（点A在点B的左侧），与
轴交于点C，且当x=－1和x=3时，的值相等．直线
与抛物线有两个交点，其中一个交点的横坐标是6，另一个交点是这条抛物线的顶点M．
(1)求这条抛物线的表达式．
(2)动点P从原点O出发，在线段OB上以每秒1个单位长度的速度向点B运动，同时动点Q从点B出发，在线段BC上以每秒
2个单位长度的速度向点C运动，当一个点到达终点时，另一个点立即停止运动，设运动时间为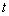
秒．
①若使△BPQ为直角三角形，请求出所有符合条件的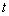值；
②求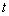为何值时，四边形ACQ P的面积有最小值，最小值是多少？
(3)如图2，当动点P运动到OB的中点时，过点P作PD⊥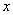
轴，交抛物线于点D，连接OD，OM，MD得△ODM，将△OPD沿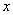轴向左平移
个单位长度（
），将平移后的三角形与△ODM重叠部分的面积记为
，求与的函数关系式．
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
在▱ABCD中，AB＜BC，已知∠B=30°，AB=2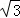
，将△ABC沿AC翻折至△AB′C，使点B′落在▱ABCD所在的平面内，连接B′D．若△AB′D是直角三角形，则BC的长为
查看答案和解析>>
科目：初中数学 来源： 题型：
一食堂需要购买盒子存放食物，盒子有A，B两种型号，单个盒子的容量和价格如表．现有15升食物需要存放且要求每个盒子要装满，由于A型号盒子正做促销活动：购买三个及三个以上可一次性返还现金4元，则购买盒子所需要最少费用为 元．
| 型号 | A | B |
| 单个盒子容量（升） | 2 | 3 |
| 单价（元） | 5 | 6 |
查看答案和解析>>
科目：初中数学 来源： 题型：
已知双曲线y=
（x＞0），直线l1：y﹣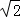
=k（x﹣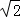）（k＜0）过定点F且与双曲线交于A，B两点，设A（x1，y1），B（x2，y2）（x1＜x2），直线l2：y=﹣x+．
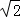（1）若k=﹣1，求△OAB的面积S；
（2）若AB=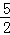
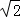，求k的值；
（3）设N（0，2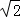），P在双曲线上，M在直线l2上且PM∥x轴，求PM+PN最小值，并求PM+PN取得最小值时P的坐标．（参考公式：在平面直角坐标系中，若A（x1，y1），B（x2，y2）则A，B两点间的距离为AB=
）
查看答案和解析>>
科目：初中数学 来源： 题型：
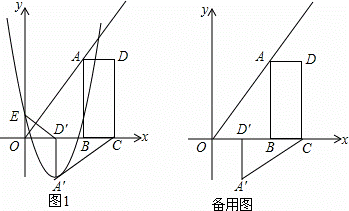
如图1，B（2m，0），C（3m，0）是平面直角坐标系中两点，其中m为常数，且m＞0，E（0，n）为y轴上一动点，以BC为边在x轴上方作矩形ABCD，使AB=2BC，画射线OA，把△ADC绕点C逆时针旋转90°得△A′D′C′，连接ED′，抛物线y=ax2+bx+n（a≠0）过E，A′两点．
（1）填空：∠AOB= 45 °，用m表示点A′的坐标：A′（ m ， ﹣m ）；
（2）当抛物线的顶点为A′，抛物线与线段AB交于点P，且
=
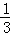时，△D′OE与△ABC是否相似？说明理由；
（3）若E与原点O重合，抛物线与射线OA的另一个交点为点M，过M作MN⊥y轴，垂足为N：
①求a，b，m满足的关系式；
②当m为定值，抛物线与四边形ABCD有公共点，线段MN的最大值为10，请你探究a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．
，由②得
③，
，
，
时，
，
．
的解集在数轴上表示正确的是（ ）
