
如图1,一条抛物线与 轴交于A,B两点(点A在点B的左侧),与
轴交于A,B两点(点A在点B的左侧),与 轴交于点C,且当x=-1和x=3时,
轴交于点C,且当x=-1和x=3时, 的值相等.直线
的值相等.直线 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
(1)求这条抛物线的表达式.
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时动点Q从点B出发,在线段BC上以每秒 2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为
2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为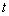 秒.
秒.
①若使△BPQ为直角三角形,请求出所有符合条件的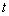 值;
值;
②求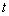 为何值时,四边形ACQ P的面积有最小值,最小值是多少?
为何值时,四边形ACQ P的面积有最小值,最小值是多少?
(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥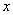 轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿
轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿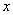 轴向左平移
轴向左平移 个单位长度(
个单位长度( ),将平移后的三角形与△ODM重叠部分的面积记为
),将平移后的三角形与△ODM重叠部分的面积记为 ,求
,求 与
与 的函数关系式.
的函数关系式.
 |
解:(1) ∵当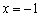 和
和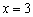 时,
时, 的值相等,∴抛物线的对称轴为直线
的值相等,∴抛物线的对称轴为直线 ,把
,把 和
和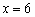 分别代入
分别代入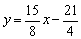 中,得顶点
中,得顶点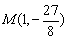 ,另一个交点坐标为(6,6), ····································································· 2分
,另一个交点坐标为(6,6), ····································································· 2分
则可设抛物线的表达式为 ,将(6,6)代入其中,解得
,将(6,6)代入其中,解得 ,
,
∴抛物线的表达式为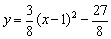 ,即
,即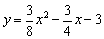 .··············································· 3分
.··············································· 3分
(2)如图1,当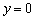 时,
时, 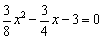 解得
解得 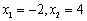 .由题意知,A(
.由题意知,A(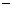 2,0),B(4,0),
2,0),B(4,0),
所以OA=2,OB=4;当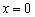 时,
时,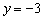 ,所以点C(0,-3),OC=3,由勾股定理知BC=5,
,所以点C(0,-3),OC=3,由勾股定理知BC=5,
 OP=1×t=t,BQ=
OP=1×t=t,BQ=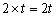 .···································································································· 4分
.···································································································· 4分
①∵∠PBQ是锐角,
∴有∠PQB=90º或∠BPQ=90º两种情况:
当∠PQB=90º时, 可得△PQB∽△COB,
∴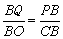 ,∴
,∴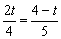 ,
,
∴ ;······························································· 5分
;······························································· 5分
当∠BPQ=90º时, 可得△BPQ∽△BOC,
∴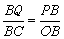 ,∴
,∴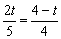 ,
,
∴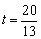 .····························································· 6分
.····························································· 6分
由题意知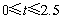 ,
,
∴当 或
或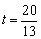 时,以B,P,Q为顶点的三角形是直角三角形. ······································ 7分
时,以B,P,Q为顶点的三角形是直角三角形. ······································ 7分
②如图1,过点Q作QG⊥AB于G, ∴△BGQ∽△BOC,
∴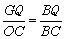 ,
,
∴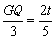 ,∴
,∴ ,····································································································· 8分
,····································································································· 8分
∴S四边形ACQP=S△ABC- S△BPQ=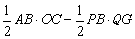 =
=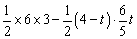
=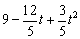 =
=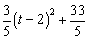 .
.
∵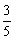 >0, ∴四边形ACQP的面积有最小值, 又∵
>0, ∴四边形ACQP的面积有最小值, 又∵ 满足
满足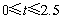 ,
,
∴当 时,四边形ACQP的面积最小,最小值是
时,四边形ACQP的面积最小,最小值是 . ····················································· 10分
. ····················································· 10分
(3)如图2,由OB=4得OP=2, 把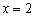 代入
代入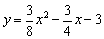 中,得
中,得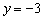 ,所以D(2, -3),直线CD∥x轴,设直线OD的解析式为
,所以D(2, -3),直线CD∥x轴,设直线OD的解析式为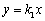 ,则
,则 ,所以
,所以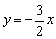 ,因为△P1O1D1是由△POD 沿x轴
,因为△P1O1D1是由△POD 沿x轴 向左平移m个单位得到的,
向左平移m个单位得到的,
所以P 1(2-m,0),D1(2-m, -3),E(2-m,
1(2-m,0),D1(2-m, -3),E(2-m,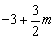 ).··········································· 11分
).··········································· 11分
设直线OM的解析式为 ,则
,则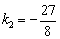 ,所以
,所以 .
.
 ①当
①当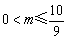 时,作FH⊥
时,作FH⊥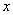 轴于点H,由题意O1(-m,0),又O1D1∥OD,所以直线O1D1的解析式为
轴于点H,由题意O1(-m,0),又O1D1∥OD,所以直线O1D1的解析式为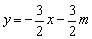 .
.
联立方程组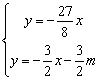 ,解得
,解得 ,
,
所以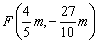 ,所以FH=
,所以FH= ,
,
S四边形OFD1E=S□OO1D1D-S△OO1F-S△DD1E
=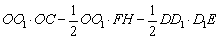
=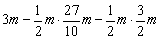 =
=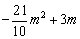 .········································································· 13分
.········································································· 13分
 ②如图3,当
②如图3,当 时,设D1P1交OM于点F,直线OM的解析式为
时,设D1P1交OM于点F,直线OM的解析式为 ,所以
,所以 ,所以
,所以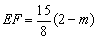 ,
,
∴S△OEF=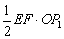 =
=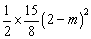 =
=
综上所述, .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:2014-2015学年江苏省滨海县八年级上学期期末考试数学试卷(解析版) 题型:选择题
已知正比例函数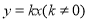 的图象经过点
的图象经过点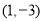 ,则此正比例函数的关系式为( ).
,则此正比例函数的关系式为( ).
A.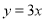 B.
B.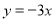 C.
C. D.
D.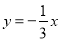
查看答案和解析>>
科目:初中数学 来源: 题型:
某化妆品专卖店,为了吸引顾客,在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满88元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):
| 甲种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金卷(元) | 6 | 12 | 6 |
| 乙种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金卷(元) | 12 | 6 | 12 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满88元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
|
| A. | “购买1张彩票就中奖”是不可能事件 |
|
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 |
|
| C. | 了解我国青年人喜欢的电视节目应作全面调查 |
|
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com