
����Ŀ����ͼ��A��0��4����ֱ������ϵy����һ�㣬����P��ԭ��O��������x���������˶����ٶ�Ϊÿ��1����λ���ȣ���PΪֱ�Ƕ����ڵ�һ������������Rt��APB����P����˶�ʱ��Ϊt�룮

��1����AB��x�ᣬ��ͼ1����t��ֵ��
��2�����A����x��ĶԳƵ�ΪA��������A��B���ڵ�P�˶��Ĺ����У���OA��B�Ķ����Ƿ�ᷢ���仯�������䣬�������OA��B�Ķ��������ı䣬��˵�����ɣ�
��3����ͼ2����t��3ʱ������ƽ������һ��M������A�غϣ�ʹ����M��P��BΪ����������κ���ABPȫ�ȣ���ֱ��д����M�����꣮
���𰸡���1��4����2����OA��B�Ķ������䣬��OA��B��![]() �����ɼ���������3����M������Ϊ��6����4������4��7������10����1��
�����ɼ���������3����M������Ϊ��6����4������4��7������10����1��
��������
��1�����õ���ֱ�������ε������Լ�ƽ���ߵ����ʣ���֤����AOPΪ����ֱ�������Σ��Ӷ���ô𰸣�
��2�����ݶԳƵ����ʵã�PA��PA'��PB���ɡ�PAB+��PBA��90��������������ڽǺͶ���������á�OA'B��45����
��3���������ۣ��ֱ����۵���ABP�ա�MBP����ABP�ա�MPB����ABP�ա�MPBʱ����M����������������M��x��Ĵ��ߡ�����B��y��Ĵ��ߣ����õ���ֱ�������ε����ʼ�ȫ�������ε��ж���������õ�M�����꼴��.
��1����AB��x�ᣬ��APBΪ����ֱ�������Σ�
���PAB����PBA����APO��45����
���AOPΪ����ֱ�������Σ�
��OA��OP��4��
��t��4��1��4���룩��
��t��ֵΪ4��
��2����ͼ2����OA��B�Ķ������䣬��OA��B��45����

�ߵ�A����x��ĶԳƵ�ΪA����
��PA��PA'��
��AP��PB��
��PA��PA'��PB��
���PAA'����PA'![]() ����PBA'����PA'B��
����PBA'����PA'B��
�֡ߡ�PAB+��PBA��90����
���PAA'+��PA'A+��PA'B+��PBA'
��180![]()
![]() 90��
90��
=90����
���AA'B��45����
����OA'B��45����
��3����t��3ʱ��M��P��BΪ����������κ���ABPȫ�ȣ�
����ͼ3������ABP�ա�MBP��
��AP��PM������M��MD��OP�ڵ�D��
�ߡ�AOP����PDM����APO����DPM��
���AOP�ա�MDP��AAS����
��OA��DM��4��OP��PD��3��
��M����������6��-4����

����ͼ4������ABP�ա�MPB����![]() ��
��
����M��M![]() ��x���ڵ�
��x���ڵ�![]() ������
������![]() ��
��![]() ��x���ڵ�
��x���ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
�ߡ�APBΪ����ֱ�������Σ����MPBҲΪ����ֱ�������Σ�
���BAP����MPB=45![]() ��
��![]()
��![]() ��
��
��![]()
��![]()
��![]()
��![]() ��x��
��x��![]() ��
��![]() ��
��
���ı���![]() Ϊ���Σ�
����
��![]() ����
����![]()
![]()
��![]() ��
��![]() ��
��
��BAF��45![]() +
+![]() ����MPE��45
����MPE��45![]() +
+![]() ��
��
���BAF����MPE
��![]()
��![]()
��![]()
��M����������4��7����

����ͼ5������ABP�ա�MPB����![]() ��
��
����M��M![]() ��x���ڵ�
��x���ڵ�![]() ������
������![]() ��
��![]() ��x���ڵ�
��x���ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
�ߡ�APBΪ����ֱ�������Σ����MPBҲΪ����ֱ�������Σ�
���BAP����MPB=45![]() ��
��![]()
��![]() ��
��
��![]()
��![]()
��![]()
��![]() ��x��
��x��![]() ��
��![]() ��
��
���ı���![]() Ϊ���Σ�
����
��![]() ����
����![]()
![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��M����������10����1����

�ۺ����Ͽɵõ�M������Ϊ����6����4������4��7������10����1����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+3��a��0����A��4��4����B��2��m�����㣬��B�������߶Գ���ľ����Ϊd������0��d��1����ʵ��m��ȡֵ��Χ�ǣ�������
A. m��2��m��3 B. m��3��m��4 C. 2��m��3 D. 3��m��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
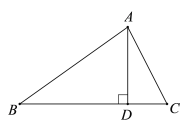
����Ŀ����ͼ����ABC�ĸ�ΪAD����A'B'C'�ĸ�ΪA'D'����A'D'��AD�����Т٢ڢ�����������
�١�B����B'����C����C'��
�ڡ�B����B'��AB��A'B'��
��BC��B'C'��AB��A'B'��
�ֱ������������������е�һ����������ж���ABC�ա�A'B'C'��д����ţ�����ͼ֤������������ж���ABC�ա�A'B'C'��д����ţ���������Ӧ�ķ���ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ��Ƽ��ķ�չ�Ѿ����뵽��5Gʱ������5G����������ƶ�ͨ�ż�����Ӣ�5th generation mobile networks��5th generation wireless systems��5th-Generation�����5G��5G������������һ�������ƶ�ͨ�ż�����Ҳ�Ǽ�4G��LTE-A��WiMax����3G��UMTS��LTE����2G��GSM��ϵͳ֮������졣�й���Ϣͨ�ſƼ���������˾����ʦ���ٻ�Ժʿ˵��ͬ4G��ȣ�5G�Ĵ������������10��100�������������˻��������ﻥ���������ﻥ�����ٵ����������ߵĽ�ϣ�5G�������ս����������ﻥ�������������� ���5G�����ֵ������4G�����ֵ���ʵ�10������ô�ڷ�ֵ�����´���1 000MB���ݣ�5G�����4G�����90�룬������������ķ�ֵ���ʣ�MB/�룩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��ʾһ������������Aд������ ����ʽ������
����ʽ������![]() ��
��![]() ��
��![]() ��
��![]() ������Ϊ�����������dzư���Aд����������ʽ��
������Ϊ�����������dzư���Aд����������ʽ��
���磺��2.8д����������ʽ�Ĺ������£�
2.8-2=0.8��![]() ��
��
1.25-1=0.25��![]() ��
��
4-4=0��

��1����3.245д����������ʽ�������Ĺ������£�
3.245-3=0.245��![]() ��
��
4.082-4=0.082��![]() ��
��
12.250-12=0.25��![]() ��
��
4-4=0��
��
��![]() _____________��
_____________��![]() _____________��
_____________��
��2�����![]() д����������ʽ��
д����������ʽ��
��3��������һ�����⣺��ͼ�dz�Ϊ47����Ϊ10�ij�����ֽƬ�����вü��������Σ���������ֽƬ��ʣ�࣬������������������Ǽ�����

С����Ϊ�������� ����һ������Ϊ��������ʽ�� �й���������![]() �����������Ӷ���������⣮����Բο�С����˼·����������⣬��ֱ��д����������������������ʱ�������εĸ�����
�����������Ӷ���������⣮����Բο�С����˼·����������⣬��ֱ��д����������������������ʱ�������εĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��BC����DΪBC��һ�㡣�ִ�����AB����һ��P����AC����һ��Q��ʹ����APQ����P��D��QΪ�����������ȫ�ȣ������Ǽס������˵�������
�ף�����AD����AD���д��߷ֱ�AB��AC��P�㡢Q�㣬��P��Q���㼴Ϊ����
�ң���D����ACƽ�е�ֱ�߽�AB��P�㣬��D����ABƽ�е�ֱ�߽�AC��Q�㣬��P��Q���㼴Ϊ����
���ڼס������˵������������жϺ�����ȷ��������?

A.���˽���ȷB.���˽Դ���C.����ȷ���Ҵ���D.�״�������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�����ʦ������������⣺
��1 ����������![]() ��
��![]() ����
����![]() �Ķ���.���𰸣�
�Ķ���.���𰸣�![]() ��
��
��2 ����������![]() ��
��![]() ����
����![]() �Ķ���.���𰸣�
�Ķ���.���𰸣�![]() ��
��![]() ��
��![]() ��
��
����ʦ����ͬѧ�ǽ��б�ʽ��С�������������⣺
��ʽ1: ����������![]() �У���A=100������
�У���A=100������![]() �Ķ���.
�Ķ���.
��ʽ2: ����������![]() �У���A= 45�� ����
�У���A= 45�� ����![]() �Ķ���.
�Ķ���.
��1������������������ʽ��.
��2���⣨1����С�����֣�![]() �Ķ�����ͬ���õ�
�Ķ�����ͬ���õ�![]() �Ķ����ĸ���Ҳ���ܲ�ͬ.����ڵ���������
�Ķ����ĸ���Ҳ���ܲ�ͬ.����ڵ���������![]() �У���
����![]() ����
����![]() ֻ��һ������ʱ������̽��
ֻ��һ������ʱ������̽��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��c��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����OB=OC=3������ΪM��
��1������κ����Ľ���ʽ��
��2����PΪ�߶�BM�ϵ�һ�����㣬����P��x��Ĵ���PQ������ΪQ����OQ=m���ı���ACPQ�����ΪS����S����m�ĺ�������ʽ����д��m��ȡֵ��Χ��
��3��̽�����߶�BM���Ƿ���ڵ�N��ʹ��NMCΪ���������Σ�������ڣ������N�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ����
����![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��

![]() ��
��![]() �ij���
�ij���
![]() ��
��![]() ���ӳ��߽�
���ӳ��߽�![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ͻ�
�ͻ�![]() Χ�ɵ�ͼ�Σ���Ӱ���֣������
Χ�ɵ�ͼ�Σ���Ӱ���֣������![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com