
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
【答案】B
【解析】
把A(4,4)代入抛物线y=ax2+bx+3得4a+b=![]() ,根据对称轴x=-
,根据对称轴x=-![]() ,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,所以0<|2-(-
,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,所以0<|2-(-![]() )|≤1,解得a≥
)|≤1,解得a≥![]() 或a≤-
或a≤-![]() ,把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,得到a=
,把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,得到a=![]() -
-![]() ,所以
,所以![]() -
-![]() ≥
≥![]() 或
或![]() -
-![]() ≤-
≤-![]() ,即可解答.
,即可解答.
把A(4,4)代入抛物线y=ax2+bx+3得:
16a+4b+3=4,
∴16a+4b=1,
∴4a+b=![]() ,
,
∵对称轴x=![]() ,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,
,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,
∴0<|2(![]() )|≤1
)|≤1
∴0<|![]() |≤1,
|≤1,
∴|![]() |≤1,
|≤1,
∴a≥![]() 或a≤
或a≤![]() ,
,
把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,
2(2a+b)+3=m,
2(2a+![]() 4a)+3=m,
4a)+3=m,
![]() 4a=m,
4a=m,
a=![]() -
-![]() ,
,
∴![]() -
-![]() ≥
≥![]() 或
或![]() -
-![]() ≤-
≤-![]() ,
,
∴m≤3或m≥4.
故答案选:B.


科目:初中数学 来源: 题型:
【题目】如图所示,某地有一座圆弧形的拱桥,桥下水面宽AB为12米,拱高CD为4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )
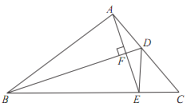
A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠O=90°,AO=18cm,BO=30cm,动点M从点A开始沿边AO以1cm/s的速度向终点O移动,动点N从点O开始沿边OB以2cm/s的速度向终点B移动,一个点到达终点时,另一个点也停止运动.如果M、N两点分别从A、O两点同时出发,设运动时间为ts时四边形ABNM的面积为Scm2.
(1)求S关于t的函数关系式,并直接写出t的取值范围;
(2)判断S有最大值还是有最小值,用配方法求出这个值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,
(1)求证:△ABC≌△EDF;
(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与探究:
如图,△ABC中,AB=AC.

(1)作图:①画线段BC的垂直平分线l,设l与BC边交于点H;
②在射线HA上画点D,使AD=AB,连接BD. (不写作法,保留作图痕迹)
(2)探究:∠D与∠C有怎样的数量关系? 并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接BE,CD,若BD=1,则△BCE的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.

(1)若AB∥x轴,如图1,求t的值;
(2)设点A关于x轴的对称点为A′,连接A′B,在点P运动的过程中,∠OA′B的度数是否会发生变化,若不变,请求出∠OA′B的度数,若改变,请说明理由.
(3)如图2,当t=3时,坐标平面内有一点M(不与A重合)使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com