
【题目】如图所示,某地有一座圆弧形的拱桥,桥下水面宽AB为12米,拱高CD为4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.

【答案】(1)这座拱桥所在圆的半径为6.5米;(2)货船不能顺利通过这座拱桥.
【解析】
(1)首先连接OA,设这座拱桥所在圆的半径为x米,由垂径定理,易得方程:x2=(x-4)2+62,解此方程即可求得答案;
(2)连接OM,设MN = 5米,可求得此时OH的高,即可求得OH-OD的长,比较3.6米,即可得到此时货船能否顺利通过这座拱桥.
(1)连结OA,
根据题意,得CD=4米,AB=12米,则AD=![]() AB=6(米).
AB=6(米).
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC-CD=(x-4)米.
在Rt△AOD中,OA2=OD2+AD2,
即x2=(x-4)2+62,
解得x=6.5,
故这座拱桥所在圆的半径为6.5米.
(2)货船不能顺利通过这座拱桥.理由:
连结OM,设MN=5米,
∵OC⊥MN,∴MH=![]() MN=2.5(米).
MN=2.5(米).
在Rt△OMH中,OH=![]() =6(米).
=6(米).
∵OD=OC-CD=6.5-4=2.5(米),
∴OH-OD=6-2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.


科目:初中数学 来源: 题型:
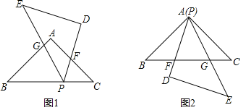
【题目】如图,![]() 、
、![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,![]() .
.
![]() 若将
若将![]() 的顶点
的顶点![]() 放在
放在![]() 上(如图
上(如图![]() ),
),![]() 、
、![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .求证:
.求证:![]() ;
;
![]() 若使
若使![]() 的顶点
的顶点![]() 与顶点
与顶点![]() 重合(如图
重合(如图![]() ),
),![]() 、
、![]() 与
与![]() 相交于点
相交于点![]() 、
、![]() .试问
.试问![]() 与
与![]() 还相似吗?为什么?
还相似吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提出问题)课间,一位同学拿着方格本遇人便问:“如图所示,在边长为1的小正方形组成的网格中,点A、B、C都是格点,如何证明点A、B、C在同一直线上呢?”

(分析问题)一时间,大家议论开了. 同学甲说:“可以利用代数方法,建立平面直角坐标系,利用函数的知识解决”,同学乙说:“也可以利用几何方法…”同学丙说:“我还有其他的几何证法”……
(解决问题)请你用两种方法解决问题
方法一(用代数方法):

方法二(用几何方法):

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是![]() 的中点,AB和DC的延长线交于⊙O外一点E.
的中点,AB和DC的延长线交于⊙O外一点E.
求证:(1)∠EBC=∠D;
(2)BC=EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:在平面直角坐标系中,将一个图形先关于y轴对称,再向下平移2个单位记为1次“R变换”.如图,已知△ABC的三个顶点均在格点上,其中点B的坐标为(1,2).

(1)画出△ABC经过1次“R变换”后的图形△A1B1C1;
(2)若△ABC经过3次“R变换”后的图形为△A3B3C3,则顶点A3坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从南京站开往上海站的一辆和谐号动车,中途只停靠苏州站,甲、乙、丙![]() 名互不相识的旅客同时从南京站上车.
名互不相识的旅客同时从南京站上车.
![]() 求甲、乙、丙三名旅客在同一个站下车的概率;
求甲、乙、丙三名旅客在同一个站下车的概率;
![]() 求甲、乙、丙三名旅客中至少有一人在苏州站下车的概率.
求甲、乙、丙三名旅客中至少有一人在苏州站下车的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com