
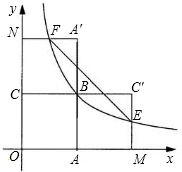
 如图,四边形OABC是面积为4的正方形,函数$y=\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为4的正方形,函数$y=\frac{k}{x}$(x>0)的图象经过点B.分析 (1)由正方形OABC的面积求出边长,进而确定出B的坐标,代入反比例解析式求出k的值即可;
(2)由题意确定出F纵坐标与E横坐标,代入反比例解析式求出相应横坐标与纵坐标,确定出E与F坐标,利用待定系数法求出直线EF解析式即可;
(3)由题意确定出C′坐标,利用待定系数法求出平移后的反比例解析式,检验即可.
解答 解:(1)由题意得:OA=AB=2,即B(2,2),
代入y=$\frac{k}{x}$得:k=4;
(2)由折叠的性质得:A′B=AB=AM=2,即A′A=4,OM=4,
∴F纵坐标为4,E横坐标为4,
把y=4代入y=$\frac{4}{x}$得:x=1;把x=4代入y=$\frac{4}{x}$得:y=1,
∴E(4,1),F(1,4),
设直线EF解析式为y=kx+b,
把E与F坐标代入得:$\left\{\begin{array}{l}{4k+b=1}\\{k+b=4}\end{array}\right.$,
解得:k=-1,b=5,
则直线EF解析式为y=-x+5;
(3)由题意得:A′(2,4),C′(4,2),
设平移后反比例解析式为y=$\frac{k′}{x}$,
把C′坐标代入得:k′=8,
∴平移后反比例解析式为y=$\frac{8}{x}$,
把x=2代入得:y=4,
则图象L1是否过点A′.
点评 此题属于反比例综合题,涉及的知识有:正方形的性质,坐标与图形性质,待定系数法确定一次函数与反比例函数解析式,熟练掌握待定系数法是解本题的关键.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:解答题
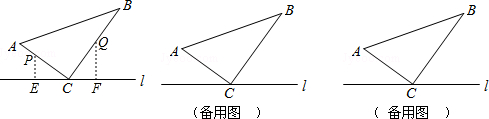
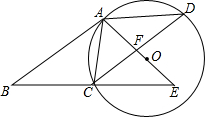 如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.
如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
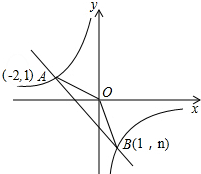 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于A(-2,1),B(1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
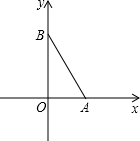 如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.
如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
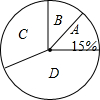 京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.
京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
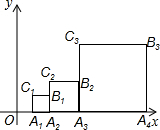 如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com