
����Ŀ������ѧ�����ʽ����ۺ������ɼ�Ϊx�֣�����Ϊ100�֣��涨��85��x��100ΪA����75��x��85ΪB����60��x��75ΪC����x��60ΪD�����������ȡij��ѧ����ѧ�����ۺ������ɼ����������Ƴ�����������������ͳ��ͼ��
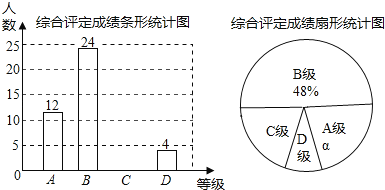
�����ͼ�е���Ϣ������������⣺
��1������ε����У�һ����ȡ���� ����ѧ����a���� ��%��C����Ӧ��Բ�Ľ�Ϊ�� ���ȣ�
��2����ȫ����ͳ��ͼ��
��3������У����2000��ѧ����������Ƹ�УD��ѧ���ж�������
���𰸡���1��50��24��72����2������������3������У����2000��ѧ�������Ƹ�УD��ѧ����160��
��������
��1������B������������ռ�İٷֱ������ȡ��������������A�����������������������a����360�����C����ռ�İٷֱȼ����������ͳ��ͼ��C����Ӧ��Բ�ĽǵĶ�����
��2���ó�ȡ����������ȥA��B��D�����������C�����������Ӷ���ȫͳ��ͼ��
��3����D����ռ�İٷֱȳ��Ը�У�������������ɵó���УD����ѧ������
�⣺��1������ε����У�һ����ȡ��ѧ�����ǣ�![]() ��50���ˣ���
��50���ˣ���
a��![]() ��100%��24%������ͳ��ͼ��C����Ӧ��Բ�Ľ�Ϊ
��100%��24%������ͳ��ͼ��C����Ӧ��Բ�Ľ�Ϊ![]() ��360����72����
��360����72����
�ʴ�Ϊ��50��24��72��
��2��C��������Ϊ��50-12-24-4=10���ˣ�
��ȫ����ͳ��ͼ��ͼ��
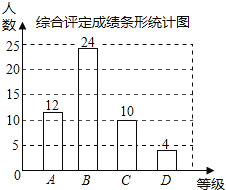
��3����2000��![]() ��160��
��160��
������У����2000��ѧ�������Ƹ�УD��ѧ����160����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B��AB��2������û��ֱ�ߣ�ֻ��һ�������Բ�棬���������뾶Ϊ1��Բ���ܷ���ƽ�����ҵ�һ��F��ʹ�á�ABF�ǵȱ������Σ�
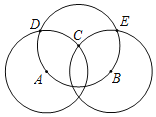
С�쾭��̽����������µ���ͼ���裺
��һ�����ֱ��Ե�A��BΪԲ�ģ�1Ϊ�뾶��Բ����Բ���ڵ�C��
�ڶ�������CΪԲ�ģ�1Ϊ�뾶��Բ����һ���е���Բ�ڵ�D��E��
���������ֱ���D��EΪԲ�ģ�1Ϊ�뾶��Բ����Բ���ڵ�C��F��
��1���뽫ͼ������������������ABF��
��2������˵���У�
����C���߶�AB�Ĵ�ֱƽ�����ϣ�
����CAD�͡�CBE���ǵȱ������Σ�
����C���߶�AF�Ĵ�ֱƽ�����ϣ�
����ABF�ǵȱ������Σ�
��ȷ������ ����������������ȷ����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
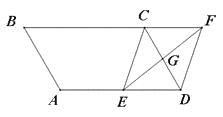
����Ŀ����7�֣���ͼ��ƽ���ı���ABCD�У�AB=3cm��BC=5cm����B=60����G��CD���е㣬E�DZ�AD�ϵĶ��㣬EG���ӳ�����BC���ӳ��߽��ڵ�F������CE��DF��
��1����֤���ı���CEDF��ƽ���ı��Σ�
��2������AE= cmʱ���ı���CEDF�Ǿ��Σ�
����AE= cmʱ���ı���CEDF�����Σ���ֱ��д���𰸣�����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ�У�����y��ax2+bx��y����bx+a��ͼ������ǣ�������
A. B.
B. C.
C.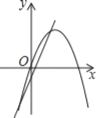 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ͳ��ȥ��1��8��������У�����ȫ��ͬѧ�Ŀ����Ķ���������λ����������������ͼ����ͳ��ͼ������˵����ȷ���ǣ� ��
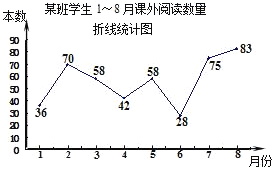
A.������47B.������42
C.��λ����58D.ÿ���Ķ���������40����4����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
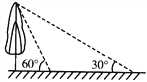
����Ŀ����ͼ��У����һ������洹ֱ��������ѧ��ȤС�����β������ڵ����ϵ�Ӱ�ӣ���һ��������������60����ʱ���ڶ���������������30����ʱ�����β�����Ӱ�����8�ף�������_____________��(�����������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
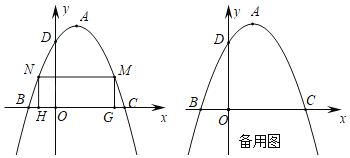
����Ŀ����ͼ����֪���κ���ͼ��Ķ�������Ϊ![]() ���������ύ��B��C��D���㣬��B�������Ϊ
���������ύ��B��C��D���㣬��B�������Ϊ![]() ��
��
��1������κ����Ľ���ʽ��
��2���ڶ��κ���ͼ��λ��x���Ϸ���������������M��N���ҵ�N�ڵ�M����࣬��M��N��x��Ĵ��߽�x���ڵ�G��H���㣬���ı���MNHGΪ����ʱ����þ����ܳ������ֵ��
��3��������MNHG���ܳ����ʱ���ܷ��ڶ��κ���ͼ�����ҵ�һ��P��ʹ![]() ������Ǿ���MNHG�����
������Ǿ���MNHG�����![]() �������ڣ�����õ�ĺ����ꣻ�������ڣ���˵�����ɣ�
�������ڣ�����õ�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
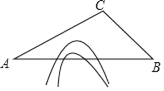
����Ŀ�������й����õĿ��ٷ�չ�Լ��Ƽ�ˮƽ�ķ�����ߣ��й�������Ѹ�����𣮸������������ʱ�վ��룬�ı������ǵij��з�ʽ����ͼ��A��B���ر���ɽ�������A�ص�B����Ҫ����C�أ�����ͨ��ɽ����������A��B���ص�ֱ��������������̴�A�ص�B�ص�·�̣���֪����CAB=30�㣬��CBA=45�㣬AC=640�����������ͨ�����ͨǰ��ȣ���A�ص�B�ص�·�̽�Լ���̶��ٹ�����ο����ݣ�![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3cm��BC=6cm.��P�ӵ�D�������A�˶����˶�����A��ֹͣ��ͬʱ����Q�ӵ�B�������C�˶����˶�����C��ֹͣ����P��Q���ٶȶ���1cm/s.����PQ��AQ��CP.���P��Q�˶���ʱ��Ϊts.
��tΪ��ֵʱ���ı���ABQP�Ǿ��Σ�
��tΪ��ֵʱ���ı���AQCP�����Σ�
�ֱ������2��������AQCP���ܳ������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com