
| A. | 当a>0时,x1<m<n<x2 | |
| B. | 当a<0时,m<x1<x2<n | |
| C. | 存在m+n=x1+x2 | |
| D. | y=ax2+bx+c-2015与x轴的交点坐标不可能是(x1,0),(x2,0) |
分析 令y=ax2+bx+c-2015,则该函数图象相当于y=ax2+bx+c向下平移2015个单位得到的,结合图象可判断选项,可得出答案.
解答 解:
方程ax2+bx+c=2015可化为ax2+bx+c-2015=0,
令y=ax2+bx+c-2015,则该函数图象相当于y=ax2+bx+c向下平移2015个单位得到,
当a>时,如图1,则有x1<m<n<x2,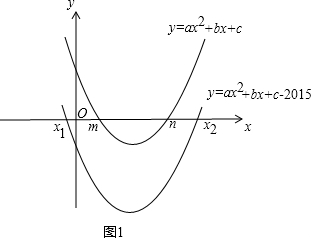
故A正确;
当a<0时,如图2,则有m<x1<x2<n,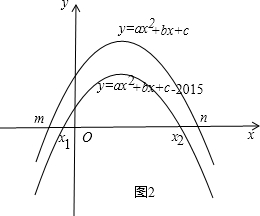
故B正确;
由两函数图象有共同的对称轴,
∴$\frac{m+n}{2}$=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{b}{2a}$,
故C正确;
∵方程ax2+bx+c=2015的两根分别为x1和x2,
∴y=ax2+bx+c-2015与x轴的交点坐标为(x1,0),(x2,0),
故D不正确;
故选D.
点评 本题主要考查二次函数与一元二次方程的关系,掌握二次函数图象的交点横坐标为对应一元二次方程的两根是解题的关键.


科目:初中数学 来源: 题型:解答题
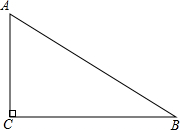 除了大家熟知的创建全国文明城市外,淮北目前也正在创建全国绿化模范城市,其中把原有的绿地扩充改造就是创建工程计划之一.如图,现有一块直角三角形的绿地,量得两直角边分别为9米和12米,需要将绿地扩大改造为等腰三角形,且扩充的部分是以BC边为直角边的直角三角形,求扩充后等腰三角形的周长.
除了大家熟知的创建全国文明城市外,淮北目前也正在创建全国绿化模范城市,其中把原有的绿地扩充改造就是创建工程计划之一.如图,现有一块直角三角形的绿地,量得两直角边分别为9米和12米,需要将绿地扩大改造为等腰三角形,且扩充的部分是以BC边为直角边的直角三角形,求扩充后等腰三角形的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
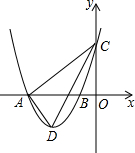 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
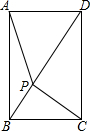 如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.
如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
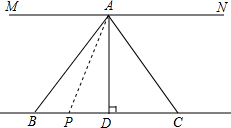 已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.
已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com