
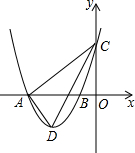
 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.分析 (1)把A(-4,0)、B(-l,0)代入y=ax2+bx+3,运用待定系数法即可求出抛物线的函数解析式;
(2)先求得直线AC的解析式,过D作DE∥y轴,交AC于点E,设D(m,$\frac{3}{4}$m2+$\frac{15}{4}$m+3),E(m,$\frac{3}{4}$m+3)(-4<m<-1),求得DE=-$\frac{3}{4}$m2-3m,根据三角形面积公式求得S=$\frac{1}{2}$DE×4=-$\frac{3}{2}$(m+2)2+6,得到S关于m的解析式,根据二次函数的解析式即可求得.
(3)以AC为直径作圆交抛物线的对称轴于P,求得AC的中点O坐标,求得对称轴方程,然后设P(-$\frac{5}{2}$,y),依据OP=$\frac{AC}{2}$=$\frac{5}{2}$,根据勾股定理得出(-2+$\frac{5}{2}$)2+($\frac{3}{2}$-y)2=($\frac{5}{2}$)2,解方程即可求得.
解答 解:(1)将A(-4,0)、B(-l,0)代入y=ax2+bx+3得
$\left\{\begin{array}{l}{16a-4b+3=0}\\{a-b+3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{3}{4}}\\{b=\frac{15}{4}}\end{array}\right.$.
故抛物线的函数解析式为y=$\frac{3}{4}$x2+$\frac{15}{4}$x+3;
(2)令x=0,则y=3,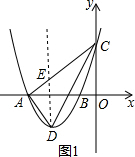
∴C(0,3),
设直线AC的解析式为y=mx+n,
代入A(-4,0)、C(0,3)得$\left\{\begin{array}{l}{-4m+n=0}\\{n=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{3}{4}}\\{n=3}\end{array}\right.$
∴AC的解析式为y=$\frac{3}{4}$x+3;
过D作DE∥y轴,交AC于点E,设D(m,$\frac{3}{4}$m2+$\frac{15}{4}$m+3),E(m,$\frac{3}{4}$m+3)(-4<m<-1),
则DE=$\frac{3}{4}$m+3-($\frac{3}{4}$m2+$\frac{15}{4}$m+3),
∴DE=-$\frac{3}{4}$m2-3m,
∴S=$\frac{1}{2}$DE×4=2(-$\frac{3}{4}$m2-3m)=-$\frac{3}{2}$m2-6m=-$\frac{3}{2}$(m+2)2+6,
∴m=-2时,S最大=6;
故m为-2时S有最大值,最大值是6.
(3)存在点P使得∠APC=90°,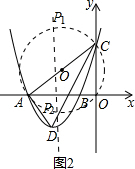
以AC为直径作圆交抛物线的对称轴于P,
∵A(-4,0)、C(0,3),
∴AC的中点O的坐标为(-2,$\frac{3}{2}$),AC=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴OP=$\frac{AC}{2}$=$\frac{5}{2}$,
∵抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,
∴对称轴x=$\frac{-4-1}{2}$=-$\frac{5}{2}$,
设P(-$\frac{5}{2}$,y),
∴OP2=($\frac{AC}{2}$)2,
(-2+$\frac{5}{2}$)2+($\frac{3}{2}$-y)2=($\frac{5}{2}$)2,
解得y=$\frac{3}{2}$±$\sqrt{6}$,
∴P的坐标为(-$\frac{5}{2}$,$\frac{3+2\sqrt{6}}{2}$)或(-$\frac{5}{2}$,$\frac{3-2\sqrt{6}}{2}$).
点评 本题是二次函数的综合题型,其中涉及到的知识点有运用待定系数法求一次函数、二次函数的解析式,直角三角形的判定,综合性较强,有一定难度.运用数形结合是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
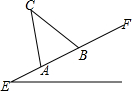 如图,为迎接全国文明城市检查,某单位准备在一斜坡EF上安装衣服悬挂“社会主义核心价值观”宣传牌的金属架A-C-B,若CA与地面垂直,斜坡的坡角∠E=30°,∠C=45°,小王测得从A到B的距离是5m,已知每米金属架106元,请你帮该单位算一下安装这副金属架共需多少元(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449,结果保留整数).
如图,为迎接全国文明城市检查,某单位准备在一斜坡EF上安装衣服悬挂“社会主义核心价值观”宣传牌的金属架A-C-B,若CA与地面垂直,斜坡的坡角∠E=30°,∠C=45°,小王测得从A到B的距离是5m,已知每米金属架106元,请你帮该单位算一下安装这副金属架共需多少元(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449,结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
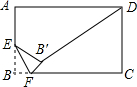 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2.
如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当a>0时,x1<m<n<x2 | |
| B. | 当a<0时,m<x1<x2<n | |
| C. | 存在m+n=x1+x2 | |
| D. | y=ax2+bx+c-2015与x轴的交点坐标不可能是(x1,0),(x2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com