
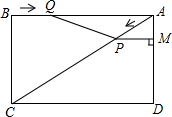
 ��֪����ͼ���ھ���ABCD�У�AC�ǶԽ��ߣ�AB=4cm��BC=3cm����P�ӵ�A��������AC���������˶����ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�B��������BA������
��֪����ͼ���ھ���ABCD�У�AC�ǶԽ��ߣ�AB=4cm��BC=3cm����P�ӵ�A��������AC���������˶����ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�B��������BA���������� ��1�����ȸ����ı���ABCD�Ǿ��Σ����AC�ij����Ƕ��٣�Ȼ����������������ж��ķ������жϳ���APQ�ס�ACB�������Ƶ�$\frac{AQ}{AB}=\frac{AP}{AC}$���ݴ����t��ֵ�Ƕ��ټ��ɣ�
��2������t=2��ʹS�ı���PQAM=$\frac{9}{50}$S����ABCD�����ȸ����ı���ABCD�Ǿ��Σ����S����ABCD��ֵ�Ƕ��٣�Ȼ��ֱ������APM����APQ��������Ƕ��٣��ٸ���S�ı���PQAM=$\frac{9}{50}$S����ABCD�����t��ֵ�Ƕ��ټ��ɣ�
��3����t=2$\frac{2}{9}$��1$\frac{7}{9}$ʱ����APQ���ABC���ƣ��������⣬������������ۣ��ٵ���AQP=90��ʱ����APQ���ABC���ƣ��ڵ���APQ=90��ʱ����APQ���ABC���ƣ������tΪ��ֵʱ����APQ���ABC���Ƽ��ɣ�
��� �⣺��1����ͼ1��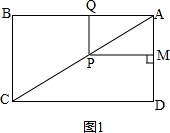 ��
��
���ı���ABCD�Ǿ��Σ�
��AC=$\sqrt{{AB}^{2}{+BC}^{2}}$=$\sqrt{{4}^{2}{+3}^{2}}$=5��
���ı���PQAM�Ǿ��Σ�
��PQ��AB��
�֡�CB��AB��
��PQ��CB��
���APQ�ס�ACB��
��$\frac{AQ}{AB}=\frac{AP}{AC}$��
��$\frac{4-t}{4}=\frac{t}{5}$��
���t=2$\frac{2}{9}$��
�൱tΪ2$\frac{2}{9}$ʱ���ı���PQAM�Ǿ��Σ�
��2������t=2��ʹS�ı���PQAM=$\frac{9}{50}$S����ABCD��
��ͼ2��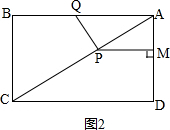 ��
��
���ı���ABCD�Ǿ��Σ�
��S����ABCD=AB•BC=4��3=12��
��PM��AD��CD��AD��
��PM��CD��
���APM�ס�ACD��
��$\frac{AM}{AD}=\frac{PM}{CD}=\frac{AP}{AC}$��
��$\frac{AM}{3}=\frac{PM}{4}=\frac{t}{5}$��
���AM=$\frac{3}{5}t$��PM=$\frac{4}{5}$t��
��S��APM=$\frac{1}{2}$AM•PM=$\frac{1}{2}��\frac{3}{5}t$��$\frac{4}{5}t$=$\frac{6}{25}$t2��
��sin��PAQ=$\frac{BC}{AC}$=$\frac{3}{5}$��
��S��APQ=$\frac{1}{2}$AP•AQ•sin��PAQ=$\frac{1}{2}$t��4-t����$\frac{3}{5}$=$\frac{3}{10}$t��4-t����
��S�ı���PQAM=$\frac{9}{50}$S����ABCD��
��$\frac{6}{25}$t2+$\frac{3}{10}$t��4-t��=$\frac{9}{50}$��$12=\frac{54}{25}$��
�������ɵ�
t2-20t+36=0
���t=2��t=18����ȥ����
�����t=2��ʹS�ı���PQAM=$\frac{9}{50}$S����ABCD��
��3����t=2$\frac{2}{9}$��1$\frac{7}{9}$ʱ����APQ���ABC���ƣ�
���ɣ�1�����ɵ�
��t=2$\frac{2}{9}$ʱ����AQP=90�㣬PQ��CB����APQ���ABC���ƣ�
����ͼ3��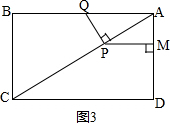 ��
��
����APQ=90��ʱ����APQ���ABC���ƣ�
��tan��PAQ=$\frac{BC}{AB}$=$\frac{3}{4}$��
��$\frac{PQ}{AP}=\frac{3}{4}$��
��$\frac{PQ}{t}=\frac{3}{4}$��
��PQ=$\frac{3}{4}$t��
��BQ=t��
��AQ=4-t��
��Rt��APQ��
��AP2+PQ2=AQ2��
��${t}^{2}{+��\frac{3}{4}t��}^{2}{=��4-t��}^{2}$��
���t=1$\frac{7}{9}$��t=-16����ȥ����
���ϣ��ɵ�
��t=2$\frac{2}{9}$��1$\frac{7}{9}$ʱ����APQ���ABC���ƣ�
���� ��1��������Ҫ���������������Ƶ��ж������ʵ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�������߷��������Ӧ�ߵı���ȵ��������������ƣ���������нǷ��������Ӧ�ߵı�����ҼнǶ�Ӧ��ȵ��������������ƣ������Ƿ���������Ƕ�Ӧ��ȵ��������������ƣ�
��2����������˾��ε����ʺ�Ӧ�ã��Լ����ɶ�����Ӧ�ã�Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7$\sqrt{2}$km | B�� | 14$\sqrt{2}$km | C�� | 7km | D�� | 14km |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
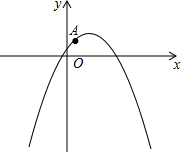 ��ֱ������ϵxoy�У���֪������$y=-\frac{{3\sqrt{3}}}{20}��{x^2}-\frac{17}{3}x-2��$��
��ֱ������ϵxoy�У���֪������$y=-\frac{{3\sqrt{3}}}{20}��{x^2}-\frac{17}{3}x-2��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
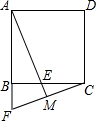 ��ͼ����������ABCD�У���ABE����ת�������CBF�غϣ�AE���ӳ��߽�FC�ڵ�M�����½�����ȷ���ǣ�������
��ͼ����������ABCD�У���ABE����ת�������CBF�غϣ�AE���ӳ��߽�FC�ڵ�M�����½�����ȷ���ǣ�������| A�� | BE=CE | B�� | FM=MC | C�� | AM��FC | D�� | BF��CF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x=3y | B�� | $\frac{y}{x}$=$\frac{2}{3}$ | C�� | $\frac{x}{2}$=$\frac{y}{3}$ | D�� | $\frac{x+y}{y}$=$\frac{5}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | 2�� | C�� | 9�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 27 | B�� | 28 | C�� | 29 | D�� | 30 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com