练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，为半圆内一点，为圆心，直径长为，，，将绕圆心逆时针旋转至，点在上，则边扫过区域(图中阴影部分)的面积为( )

    A. B. C. D.

    【答案】A

    【解析】

    根据已知条件和旋转的性质得出两个扇形的圆心角的度数，再根据扇形的面积公式进行计算即可得出答案．

    ∵∠BOC=60°，△B′OC′是△BOC绕圆心O逆时针旋转得到的，

    ∴∠B′OC′=60°，△BCO=△B′C′O，

    ∴∠B′OC=60°，∠C′B′O=30°，

    ∴∠B′OB=120°，

    ∵AB=4cm，

    ∴OB21cm，OC′=1，

    ∴B′C′=，

    ∴S扇形B′OB=，

    S扇形C′OC=，

    ∴阴影部分面积=S扇形B′OB+S△B′C′O-S△BCO-S扇形C′OC=S扇形B′OB-S扇形C′OC==π；

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝a（x+1）（x﹣3）与x轴交于A、B两点，抛物线与x轴围成的封闭区域（不包含边界），仅有4个整数点时（整数点就是横纵坐标均为整数的点），则a的取值范围_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

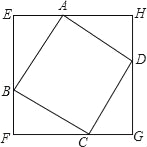
    【题目】如图，正方形ABCD的四个顶点分别在正方形EFGH的四条边上，我们称正方形EFGH是正方形ABCD的外接正方形．

    探究一：巳知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍？如图，假设存在正方形EFGH，它的面积是正方形ABCD的2倍．

    因为正方形ABCD的面积为1，则正方形EFGH的面积为2，

    所以EF=FG=GH=HE=，设EB=x，则BF=﹣x，

    ∵Rt△AEB≌Rt△BFC

    ∴BF=AE=﹣x

    在Rt△AEB中，由勾股定理，得

    x2+（﹣x）2=12

    解得，x1=x2=

    ∴BE=BF，即点B是EF的中点．

    同理，点C，D，A分别是FG，GH，HE的中点．

    所以，存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍

    探究二：巳知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍？（仿照上述方法，完成探究过程）

    探究三：巳知边长为1的正方形ABCD，　 　一个外接正方形EFGH，它的面积是正方形ABCD面积的4倍？（填“存在”或“不存在”）

    探究四：巳知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的n倍？（n＞2）（仿照上述方法，完成探究过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲.乙两人进行跑步训练，他们所跑的路程y（米）与时间x（秒）之间的关系如图所示，则下列说法错误的是（　 ）

    A. 离终点40米处，乙追上甲B. 甲比乙迟3秒到终点

    C. 甲跑步的速度是5米/秒D. 乙跑步的速度是米/秒

    查看答案和解析>>

    科目：初中数学 来源： 题型：

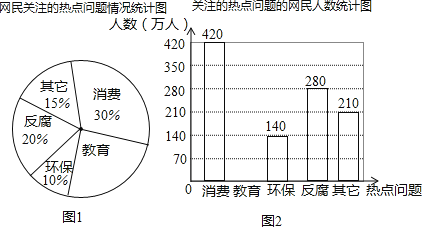
    【题目】某调查机构将今年绍兴市民最关注的热点话题分为消费.教育.环保.反腐及其它共五类．根据最近一次随机调查的相关数据，绘制的统计图表如下：

    根据以上信息解答下列问题：

    （1）本次共调查_________人，请在答题卡上补全条形统计图并标出相应数据；

    （2）若绍兴市约有500万人口，请你估计最关注教育问题的人数约为多少万人？

    （3）在这次调查中，某单位共有甲.乙.丙.丁四人最关注教育问题，现准备从这四中随机抽取两人进行座谈，求抽取的两人恰好是甲和乙的概率（画树状图或列表说明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是的弦，为半径的中点，过作交弦于点，交于点，且是的切线.

    (1)求证：；

    (2)连接，，求；

    (3)如果，，，求的半径.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

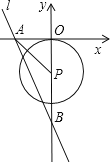
    【题目】如图，在平面直角坐标系中，直线l：y=-2x-8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P．

    （1）若⊙P与x轴有公共点，则k的取值范围是______．

    （2）连接PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；

    （3）当⊙P与直线l相切时，k的值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市某中学积极响应创建全国文明城市活动，举办了以“校园文明”为主题的手抄报比赛.所有参赛作品均获奖，奖项分为一等奖、二等奖、三等奖和优秀奖，将获奖结果绘制成如右两幅统计图.请你根据图中所给信息解答意）

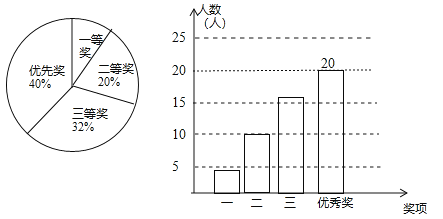
    （1）等奖所占的百分比是________；三等奖的人数是________人；

    （2）据统计，在获得一等奖的学生中，男生与女生的人数比为，学校计划选派1名男生和1名女生参加市手抄报比赛，请求出所选2位同学恰是1名男生和1名女生的概率；

    （3）学校计划从获得二等奖的同学中选取一部分人进行集训使其提升为一等奖，要使获得一等奖的人数不少于二等奖人数的2倍，那么至少选取多少人进行集训？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：我们知道，在四边形ABCD中，当对角线，若，时，

    （1）则四边形ABCD的面积为 ；

    小凯遇到一个问题：如图1，在四边形ABCD中，对角线AC、BD相交于点O，，，，求四边形ABCD的面积。

    小凯发现，如图2分别过点A、C作直线BD的垂线，垂足分别为点E，F，设AO为m，通过计算与的面积和使问题得以解决。

    请回答：

    （2）的面积为 （用含m的式子表示）

    （3）求四边形ABCD的面积。

    参考小凯思考问题的方法，解决问题：如图3，在四边形ABCD中，对角线AC、BD相交于点O，，，（），则四边形ABCD的面积为 （用含a，b，的式子表示）

    查看答案和解析>>

    同步练习册答案