
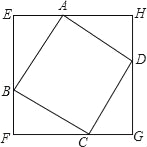
【题目】如图,正方形ABCD的四个顶点分别在正方形EFGH的四条边上,我们称正方形EFGH是正方形ABCD的外接正方形.
探究一:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍?如图,假设存在正方形EFGH,它的面积是正方形ABCD的2倍.
因为正方形ABCD的面积为1,则正方形EFGH的面积为2,
所以EF=FG=GH=HE=![]() ,设EB=x,则BF=
,设EB=x,则BF=![]() ﹣x,
﹣x,
∵Rt△AEB≌Rt△BFC
∴BF=AE=![]() ﹣x
﹣x
在Rt△AEB中,由勾股定理,得
x2+(![]() ﹣x)2=12
﹣x)2=12
解得,x1=x2=![]()
∴BE=BF,即点B是EF的中点.
同理,点C,D,A分别是FG,GH,HE的中点.
所以,存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍
探究二:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的3倍?(仿照上述方法,完成探究过程)
探究三:巳知边长为1的正方形ABCD, 一个外接正方形EFGH,它的面积是正方形ABCD面积的4倍?(填“存在”或“不存在”)
探究四:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的n倍?(n>2)(仿照上述方法,完成探究过程)
【答案】不存在,详见解析
【解析】
探究二,根据探究一的解答过程、运用一元二次方程计算即可;探究三,根据探究一的解答过程、运用一元二次方程根的判别式解答;探究四,根据探究一的解答过程、运用一元二次方程根的判别式解答.
探究二:因为正方形ABCD的面积为1,则正方形EFGH的面积为3,
所以EF=FG=GH=HE=![]() ,设EB=x,则BF=
,设EB=x,则BF=![]() ﹣x,
﹣x,
∵Rt△AEB≌Rt△BFC,
∴BF=AE=![]() ﹣x,
﹣x,
在Rt△AEB中,由勾股定理,得,
x2+(![]() ﹣x)2=12,
﹣x)2=12,
整理得x2﹣![]() x+1=0,
x+1=0,
b2﹣4ac=3﹣4<0,
此方程无解,
不存在一个外接正方形EFGH,它的面积是正方形ABCD面积的3倍;
探究三:因为正方形ABCD的面积为1,则正方形EFGH的面积为4,
所以EF=FG=GH=HE=2,设EB=x,则BF=2﹣x,
∵Rt△AEB≌Rt△BFC,
∴BF=AE=2﹣x,
在Rt△AEB中,由勾股定理,得,
x2+(2﹣x)2=12,
整理得2x2﹣4x+3=0,
b2﹣4ac=16﹣24<0,
此方程无解,
不存在一个外接正方形EFGH,它的面积是正方形ABCD面积的3倍,
故答案为:不存在;
探究四:因为正方形ABCD的面积为1,则正方形EFGH的面积为n,
所以EF=FG=GH=HE=![]() ,设EB=x,则BF=
,设EB=x,则BF=![]() ﹣x,
﹣x,
∵Rt△AEB≌Rt△BFC,
∴BF=AE=![]() ﹣x,
﹣x,
在Rt△AEB中,由勾股定理,得,
x2+(![]() ﹣x)2=12,
﹣x)2=12,
整理得2x2﹣2![]() x+n﹣1=0,
x+n﹣1=0,
b2﹣4ac=8﹣4n<0,
此方程无解,
不存在一个外接正方形EFGH,它的面积是正方形ABCD面积的n倍.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】某校九年级有24个班,共1 000名学生,他们参加了一次数学测试.学校统计了所有学生的成绩,得到下列统计图.

(1)求该校九年级学生本次数学测试成绩的平均数;
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设快车离乙地的距离为y1(km),慢车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km).y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.则下列判断:①图1中a=3;②当x=![]() h时,两车相遇;③当x=
h时,两车相遇;③当x=![]() 时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=
时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=![]() h或
h或![]() h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)
h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
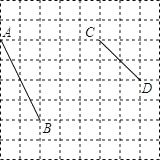
【题目】如图,在小正方形的边长均为1的方格纸中,有线段![]() 和线段
和线段![]() ,点
,点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
(1)在方格纸中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点E在小正方形的顶点上,且
,点E在小正方形的顶点上,且![]() 的面积为5;
的面积为5;
(2)在方格纸中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在小正方形的顶点上,
在小正方形的顶点上,![]() 的面积为4,射线
的面积为4,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为2m,宽为1.2m的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)若长方体底面面积为1.28m2,求裁掉的正方形边长;
(2)若要求制作的长方体的底面长不大于底面宽的3倍,并将容器进行防锈处理,侧面每平方米的费用为50元,底面每平方米的费用为200元,裁掉的正方形边长多大时,总费用最低,最低为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
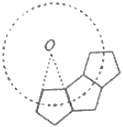
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△AOB和△A1OB1是以点O为位似中心的位似图形,且△AOB和△A1OB1的周长之比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )
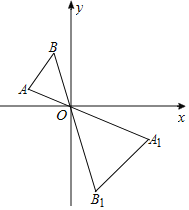
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com