
【题目】已知,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的上边作正方形ADEF,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: . 
(2)数学思考:如图2,当点D在线段CB的延长线上时,以上①②关系是否成立,请在后面的横线上写出正确的结论.①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: . 
(3)如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GD,若已知AB=2 ![]() ,CD=
,CD= ![]() BC,请求出DG的长(写出求解过程).
BC,请求出DG的长(写出求解过程).
【答案】
(1)BC⊥CF;CF=BC-CD
(2)BC⊥CF;CF=CD﹣BC
(3)
解:由题意得:∠BAC=∠FAD=90°,∴∠BAD=∠CAF,
在△BAD和△CAF中, 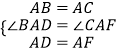 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠FCB=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BC,
在Rt△ABC中,AC=AB=2 ![]() ,
,
在Rt△AGC中,∵∠ACF=45°,
∴CG= ![]() AC=
AC= ![]() ×2
×2 ![]() =4,
=4,
同理BC=4,
CD= ![]() BC=
BC= ![]() ×4=1,
×4=1,
∴在Rt△DCG中,DG= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)证明:①∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°,∴∠BAD=∠CAF,在△BAD和△CAF中, 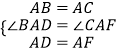 ,∴△BAD≌△CAF(SAS),∴∠ACF=∠ABD=45°,∴∠ACF+∠ACB=90°,∴∠BCF=90°,∴BC⊥CF,所以答案是:BC⊥CF;②由①△BAD≌△CAF,∴BD=CF,∵BD=BC﹣CD,∴CF=BC﹣CD,所以答案是:CF=BC﹣CD;
,∴△BAD≌△CAF(SAS),∴∠ACF=∠ABD=45°,∴∠ACF+∠ACB=90°,∴∠BCF=90°,∴BC⊥CF,所以答案是:BC⊥CF;②由①△BAD≌△CAF,∴BD=CF,∵BD=BC﹣CD,∴CF=BC﹣CD,所以答案是:CF=BC﹣CD;
⑵解:①成立,②不成立;理由如下:①∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAC=∠BAF+∠FAC=90°,∠DAF=∠BAF+∠DAB=90°,∴∠BAD=∠CAF,在△BAD和△CAF中, 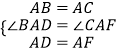 ,∴△BAD≌△CAF(SAS),∴∠ACF=∠ABD=180°﹣45°=135°,∴∠ACB+∠FCB=135°,∴∠FCB=90°,∴BC⊥CF,所以答案是:BC⊥CF;②由①△BAD≌△CAF,∴BD=CF,∵BD=CD﹣BC,∴CF=CD﹣BC,所以答案是:CF=CD﹣BC;
,∴△BAD≌△CAF(SAS),∴∠ACF=∠ABD=180°﹣45°=135°,∴∠ACB+∠FCB=135°,∴∠FCB=90°,∴BC⊥CF,所以答案是:BC⊥CF;②由①△BAD≌△CAF,∴BD=CF,∵BD=CD﹣BC,∴CF=CD﹣BC,所以答案是:CF=CD﹣BC;
【考点精析】根据题目的已知条件,利用垂线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ= ![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生在家使用电脑的情况(分为“总是、较多、较少、不用”四种情况),随机在八、九年级各抽取相同数量的学生进行调查,绘制成部分统计图如下所示.请根据图中信息,回答下列问题: 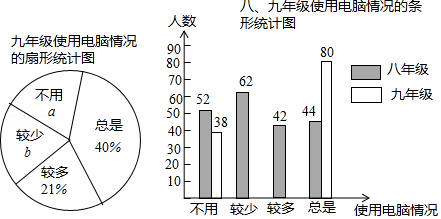
(1)九年级一共抽查了名学生,图中的a= , “总是”对应的圆心角为度.
(2)根据提供的信息,补全条形统计图.
(3)若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b>
交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集.
的解集. 
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
艾斯柯同学类比以上知识的研究方法,用函数与方程的思想对不等式的解法进行了探究,请将他下面的②③④补充完整:
①当x=0时,原不等式不成立:当x>0时,原不等式可以转化为x2+4x﹣1> ![]() ;当x<0时,原不等式可以转化为x2+4x﹣1<
;当x<0时,原不等式可以转化为x2+4x﹣1< ![]() .
.
②构造函数,画出图象
设y3=x2+4x﹣1,y4= ![]() 在同一坐标系中分别画出这两个函数的图象.
在同一坐标系中分别画出这两个函数的图象.
双曲线y4= ![]() 如图2所示,请在此坐标系中直接画出抛物线y3=x2+4x﹣1(可不列表);
如图2所示,请在此坐标系中直接画出抛物线y3=x2+4x﹣1(可不列表);
③利用图象,确定交点横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ![]()
④借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= ![]() 在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( ) 
A.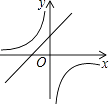
B.
C.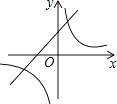
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,
求证:四边形ABCD是四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为平行四边形两组对边分别相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com