Question

【题目】抛物线y=ax2+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y= 在同一平面直角坐标系内的图象大致为（ ）
A.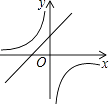
B.
C.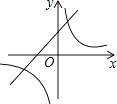
D.

Answer 1

【答案】B
【解析】解：由抛物线可知，a＞0，b＜0，c＜0， ∴一次函数y=ax+b的图象经过第一、三、四象限，
反比例函数y= 的图象在第二、四象限，
故选：B．
【考点精析】根据题目的已知条件，利用一次函数的图象和性质和反比例函数的图象的相关知识可以得到问题的答案，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点．