
【题目】如图,AB是⊙O的直径,OB=3,BC是⊙O的弦,∠ABC的平分线交⊙O于点D,连接OD,若∠BAC=20°,则 ![]() 的长等于 .
的长等于 . 
【答案】![]() π
π
【解析】解:∵AB是⊙O的直径, ∴∠ACB=90°,
∵∠BAC=20°,
∴∠ABC=90°﹣20°=70°,
∵∠ABC的平分线交⊙O于点D,
∴∠ABD= ![]() ∠ABC=
∠ABC= ![]() ×70°=35°,
×70°=35°,
∴∠AOD=2∠ABD=2×35°=70°,
∴ ![]() 的长=
的长= ![]() =
= ![]() π.
π.
所以答案是: ![]() π.
π.
【考点精析】本题主要考查了圆周角定理和弧长计算公式的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A,B在函数y= ![]() (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
①当k=2时,正方形A′B′C′D′的边长等于 .
②当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( ) 
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产50件
D.若工人乙一天生产m(件),则他获得薪金4m元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA. 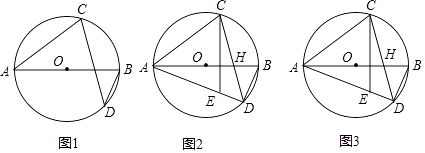
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深入贯彻党的十八大精神,我省某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为A,B,C,D,E五个组,x表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
A组:90≤x≤100 B组:80≤x<90 C组:70≤x<80 D组:60≤x<70 E组:x<60
(1)参加调查测试的学生共有人;请将两幅统计图补充完整.
(2)本次调查测试成绩的中位数落在组内.
(3)本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的上边作正方形ADEF,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: . 
(2)数学思考:如图2,当点D在线段CB的延长线上时,以上①②关系是否成立,请在后面的横线上写出正确的结论.①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: . 
(3)如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GD,若已知AB=2 ![]() ,CD=
,CD= ![]() BC,请求出DG的长(写出求解过程).
BC,请求出DG的长(写出求解过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com