
【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA. 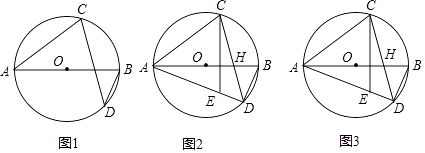
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
【答案】
(1)解:如图1,设∠BDC=α,∠DAC=β,
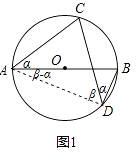
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴ ![]() =
= ![]() ,
,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)解:∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
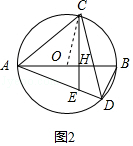
(3)解:如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BEC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴ ![]() ,
,
∵OH=5,
∴BD=10,
∴AB= ![]() =26,
=26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AE= ![]() ,
,
∴DE= ![]() .
.
【解析】(1)如图1,设∠BDC=α,∠DAC=β,根据圆周角定理得到∠CAB=∠BDC=α,连接AD,由AB为⊙O直径,得到∠ADB=90°,根据余角的性质即可得到结论;(2)根据已知条件得到∠ACE=∠ADC,等量代换得到∠ACE=∠CAE,于是得到结论;(3)如图2,连接OC,根据圆周角定理得到∠COB=2∠CAB,等量代换得到∠COB=∠ABD,根据相似三角形的性质得到OH=5,根据勾股定理得到AB= ![]() =26,由相似三角形的性质即可得到结论.
=26,由相似三角形的性质即可得到结论.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣ ![]() x﹣
x﹣ ![]() 与x轴交于点A,与y轴交于点C,抛物线y=ax2﹣
与x轴交于点A,与y轴交于点C,抛物线y=ax2﹣ ![]() x+c(a≠0)经过A,B,C三点.
x+c(a≠0)经过A,B,C三点.
(1)求过A,B,C三点抛物线的解析式并求出顶点F的坐标;
(2)在抛物线上是否存在点P,使△ABP为直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由;
(3)试探究在直线AC上是否存在一点M,使得△MBF的周长最小?若存在,求出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.
(1)如图1,求证:AE=BD; 
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数y=
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数y= ![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数y= ![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点O为坐标原点,直线y= ![]() x+1与抛物线y=
x+1与抛物线y= ![]() x2+bx+c交于A,B两点,点A在x轴上,点B的横坐标为4.
x2+bx+c交于A,B两点,点A在x轴上,点B的横坐标为4.
(1)求抛物线的解析式;
(2)抛物线y= ![]() x2+bx+c 交x轴正半轴于点C,横坐标为t的点P在第四象限的抛物线上,过点P作AB的垂线交x轴于点E,点Q为垂足,设CE的长为d,求d与t之间的函数关系式,直接写出自变量t的取值范围:
x2+bx+c 交x轴正半轴于点C,横坐标为t的点P在第四象限的抛物线上,过点P作AB的垂线交x轴于点E,点Q为垂足,设CE的长为d,求d与t之间的函数关系式,直接写出自变量t的取值范围:
(3)在(2)的条件下,过点B作y轴的平行线交x轴于点D,连接DQ.当∠AQD=3∠PQD时,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生在家使用电脑的情况(分为“总是、较多、较少、不用”四种情况),随机在八、九年级各抽取相同数量的学生进行调查,绘制成部分统计图如下所示.请根据图中信息,回答下列问题: 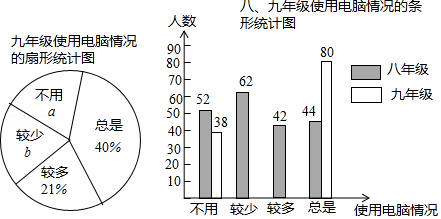
(1)九年级一共抽查了名学生,图中的a= , “总是”对应的圆心角为度.
(2)根据提供的信息,补全条形统计图.
(3)若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
(1)点B的坐标为;用含t的式子表示点P的坐标为;
(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值?
(3)试探究:在上述运动过程中,是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC的 ![]() ?若存在,求出点T的坐标;若不存在,请说明理由.
?若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com