
【题目】如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
(1)点B的坐标为;用含t的式子表示点P的坐标为;
(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值?
(3)试探究:在上述运动过程中,是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC的 ![]() ?若存在,求出点T的坐标;若不存在,请说明理由.
?若存在,求出点T的坐标;若不存在,请说明理由.
【答案】
(1)(6,4);(t, ![]() t)
t)
(2)
解:∵S△OMP= ![]() ×OM×
×OM× ![]() t,
t,
∴S= ![]() ×(6﹣t)×
×(6﹣t)× ![]() t=﹣
t=﹣ ![]() t2+2t=﹣
t2+2t=﹣ ![]() (t﹣3)2+3(0<t<6).
(t﹣3)2+3(0<t<6).
∴当t=3时,S有最大值.
(3)
解:存在.理由如下:
由(2)得,当S有最大值时,点M、N的坐标分别为:M(3,0),N(3,4),
则直线ON的函数关系式为:y= ![]() x.
x.
设点T的坐标为(0,b),则直线MT的函数关系式为:y=﹣ ![]() x+b,
x+b,
解方程组 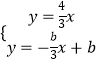 得
得 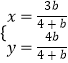 ,
,
∴直线ON与MT的交点R的坐标为( ![]() ,
, ![]() ),
),
∵S△OCN= ![]() ×4×3=6,
×4×3=6,
∴S△ORT= ![]() S△OCN=2,
S△OCN=2,
①当点T在点O、C之间时,分割出的三角形是△OR1T1,
如图2所示,作R1D1⊥y轴,D1为垂足,则S△OR1T1= ![]() RD1OT=
RD1OT= ![]()
![]() b=2.
b=2.
∴3b2﹣4b﹣16=0,
解得:b= ![]() (负值舍去).
(负值舍去).
∴b= ![]() ,
,
此时点T1的坐标为(0, ![]() ).
).
②当点T在OC的延长线上时,分割出的三角形是△R2NE,如图,设MT交CN于点E,
由①得点E的横坐标为 ![]() ,作R2D2⊥CN交CN于点D2,则
,作R2D2⊥CN交CN于点D2,则
S△R2NE= ![]() ENR2D2=
ENR2D2= ![]() (3﹣
(3﹣ ![]() )(4﹣
)(4﹣ ![]() =
= ![]() =2.
=2.
∴b2+4b﹣48=0,
解得:b=±2 ![]() ﹣2(负值舍去).
﹣2(负值舍去).
∴b=2 ![]() ﹣2.
﹣2.
∴此时点T2的坐标为(0,2 ![]() ).
).
综上所述,在y轴上存在点T1(0, ![]() ),T2(0,2
),T2(0,2 ![]() ﹣2)符合条件.
﹣2)符合条件.
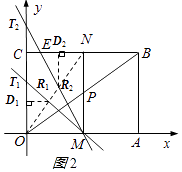
【解析】解:(1)延长NP交OA于H,如图1所示:
∵矩形OABC,
∴BC∥OA,∠OCB=90°,
∵PN⊥BC,
∴NH∥OC,
∴四边形CNHO是平行四边形,
∴OH=CN,
∵OA=6,AB=4,
∴点B的坐标为(6,4);
由图可得,点P的横坐标=0H=CN=t,纵坐标=4﹣NP,
∵NP⊥BC,
∴NP∥OC,
∴NP:OC=BN:CB,
即NP:4=(6﹣t):6,
∴NP=4﹣ ![]() t,
t,
∴点P的纵坐标=4﹣NP= ![]() t,
t,
则点P的坐标为(t, ![]() t);
t);
所以答案是:(6,4);(t, ![]() t);
t);
【考点精析】根据题目的已知条件,利用二次函数的最值和平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA. 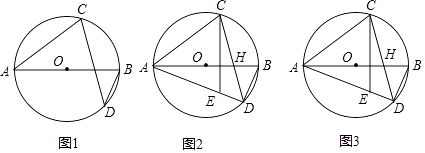
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E. 
(1)求证:∠MDE=∠MED;
(2)填空: ①若AB=6,当DM=2AD时,DE=;
②连接OD、OE,当∠C的度数为时,四边形ODME是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平行四边形ABCD中,∠B=60°,将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,角的两边所在的两直线分别交线段AB、AD于点E、F(不包括线段的端点).
(1)问题发现:
如图1,若平行四边形ABCD为菱形,
试猜想线段AE、AF、AC之间的数量关系 ![]() ,请证明你的猜想.
,请证明你的猜想.
(2)类比探究:
如图2,若AB:AD=1:2,过点C作CH⊥AD于点H,求AE:FH的比值;
(3)拓展延伸:
如图3,若AB:AD=1:4,请直接写出(AE+4AF):AC的比值为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家环保局统一规定,空气质量分为5级:1级质量为优;2级质量为良;3级质量为轻度污染;4级质量为中度污染;5级质量为重度污染.某城市随机抽取了一年中某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题: 
(1)本次调查共抽取了天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为°;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计该年该城市只有多少天适宜户外活动.(一年天数按365天计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2的单位,这种点的运动称为点A的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5),已知点A的坐标为(1,0).
(1)分别写出点A经1次,2次斜平移后得到的点的坐标.
(2)如图,点M是直线l上的一点,点A关于点M的对称点的点B,点B关于直线l的对称轴为点C.
①若A、B、C三点不在同一条直线上,判断△ABC是否是直角三角形?请说明理由.
②若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),求出点B的坐标及n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E两点,经测量AD=10cm,BE=15cm, 则该自来水管的半径为( )cm.
A.5
B.10
C.6
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com