
【题目】已知,菱形ABCD中,E,F分别是对角线BD和边BC上一点,且满足∠EAF=∠ABD=![]() .
.
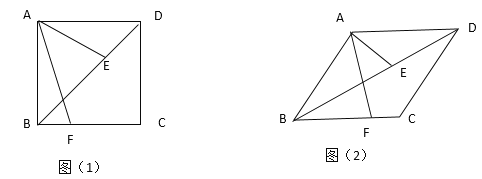
(1)如图(1),当![]() =45°时,求证:AF=
=45°时,求证:AF=![]() AE
AE
(2)如图(2),探究AF与AE的数量关系(用含![]() 的锐角三角函数表示)
的锐角三角函数表示)
【答案】(1)见解析;(2)AF=2AEcos![]()
【解析】
(1)连接AC,证明△AFC∽△AED,由相似三角形的性质,即可得到答案;
(2)设AF与BE交于点G,作EH⊥AF于H,由菱形的性质,以及相似三角形的判定和性质,得到AE=EF,由三角函数即可得到答案.
解:(1)连结AC,
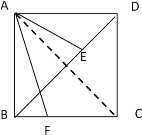
当![]() =45°时,
=45°时,
∴∠EAF=∠ABD=45°,
∴四边形ABCD正方形,
∴∠ACF=∠ADE=∠DAC=45°,
∴∠EAF=∠DAC=45°,
∴∠CAF=∠DAE,
∴△AFC∽△AED ,
∴![]()
∴![]() ;
;
(2)设AF与BE交于点G,
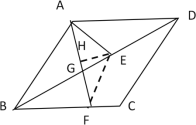
∵∠EAF=∠ABD=![]()
又菱形ABCD
∴∠EAF=∠ABD=∠FBG=![]()
∵∠BGF=∠AGE
∴△AGE∽△BGF
∴![]() ,
,
∵∠BGA=∠FGE
∴△AGB∽△EGF
∴∠EFG=∠ABG=![]()
∴AE=EF
作EH⊥AF于H
∵![]() ,
,
∴AH=AEcos![]()
∴ AF=2AEcos![]() ;
;


科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,按学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:
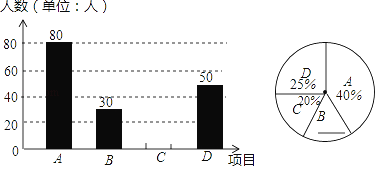
(1)本次共调查了________名学生;
(2)在扇形统计图中,“B”所在扇形的圆心角是________度;
(3)将条形统计图补充完整;
(4)若该中学有1200名学生,喜欢篮球运动的学生约有________名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴的正半轴交于点A,与
轴的正半轴交于点A,与![]() 轴的负半轴交于点B,
轴的负半轴交于点B, ![]() ,过点A作
,过点A作![]() 轴的垂线与过点O的直线相交于点C,直线OC的解析式为
轴的垂线与过点O的直线相交于点C,直线OC的解析式为![]() ,过点C作
,过点C作![]() 轴,垂足为
轴,垂足为![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;
(2)如图2,点N在线段![]() 上,连接ON,点P在线段ON上,过P点作
上,连接ON,点P在线段ON上,过P点作![]() 轴,垂足为D,交OC于点E,若
轴,垂足为D,交OC于点E,若![]() ,求
,求![]() 的值;
的值;
(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作![]() 轴的平行线交BQ于点G,连接PF交
轴的平行线交BQ于点G,连接PF交![]() 轴于点H,连接EH,若
轴于点H,连接EH,若![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=ax2﹣2ax+c的图象经过点A(﹣1,1),将A点向右平移3个单位长度,再向上平移2个单位长度,得到点B,直线y=2x+m经过点B,与y轴交于点C.
(1)求点B,C的坐标;
(2)求二次函数图象的对称轴;
(3)若二次函数y=ax2﹣2ax+c(﹣1<x<2)的图象与射线CB恰有一个公共点,结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
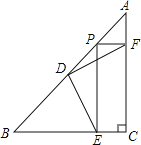
(1)探究DE与DF的关系,并给出证明;
(2)当点P满足什么条件时,线段EF的长最短?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
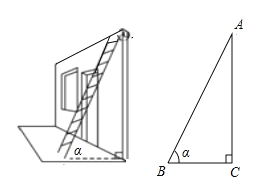
【题目】如图.要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角![]() 一般要满足
一般要满足![]() ,现有一架长
,现有一架长![]() 的梯子.
的梯子.
(1)使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?
(2)当梯子底端距离墙面![]() 时,
时,![]() 等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?
等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线![]() ,点A、B分别在
,点A、B分别在![]() 、
、![]() 上,斜坡AB的长为18米,过点B作
上,斜坡AB的长为18米,过点B作![]() 于点C,且线段AC的长为
于点C,且线段AC的长为![]() 米.
米.
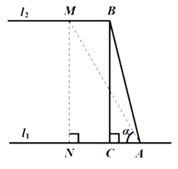
(1)求该斜坡的坡高BC;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚![]() 为60°,过点M作
为60°,过点M作![]() 于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,![]() ,D、E分别是边AB、BC上的动点,且
,D、E分别是边AB、BC上的动点,且![]() ,连结AD、AE,点M、N、P分别是CD、AE、AC的中点,设
,连结AD、AE,点M、N、P分别是CD、AE、AC的中点,设![]() .
.
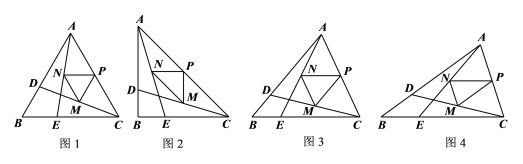
(1)观察猜想
①在求![]() 的值时,小明运用从特殊到一般的方法,先令
的值时,小明运用从特殊到一般的方法,先令![]() ,解题思路如下:
,解题思路如下:
如图1,先由![]() ,得到
,得到![]() ,再由中位线的性质得到
,再由中位线的性质得到![]() ,
,
![]() ,进而得出△PMN为等边三角形,∴
,进而得出△PMN为等边三角形,∴![]() .
.
②如图2,当![]() ,仿照小明的思路求
,仿照小明的思路求![]() 的值;
的值;
(2)探究证明
如图3,试猜想![]() 的值是否与
的值是否与![]() 的度数有关,若有关,请用含
的度数有关,若有关,请用含![]() 的式子表示出
的式子表示出![]() ,若无关,请说明理由;
,若无关,请说明理由;
(3)拓展应用
如图4,![]() ,点D、E分别是射线AB、CB上的动点,且
,点D、E分别是射线AB、CB上的动点,且![]() ,点M、N、P分别是线段CD、AE、AC的中点,当
,点M、N、P分别是线段CD、AE、AC的中点,当![]() 时,请直接写出MN的长.
时,请直接写出MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
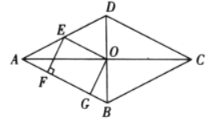
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com