练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
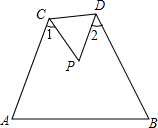
    13．如图，△ABP沿CD折叠，求证：∠1+∠2=2∠P．

    分析 根据翻折变换的性质得到∠3=∠4，∠5=∠6，根据三角形内角和定理得到∠P=180°-（∠A+∠B），根据四边形内角和等于360°代入计算即可．

    解答 证明：由折叠可得，∠3=∠4，∠5=∠6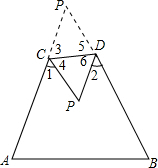
    ∵∠A+∠B+∠P=180°∠P+∠3+∠5=180°，
    ∴∠A+∠B=∠3+∠5=∠4+∠6，
    ∴∠P=180°-（∠A+∠B），
    又∵∠A+∠B+∠BDC+∠DCA=360°，
    ∴∠A+∠B+∠1+∠2+∠4+∠6=360°，
    ∴2（∠A+∠B）+（∠1+∠2）=360°，
    ∴∠1+∠2=360°-2（180°-∠P）=2∠P．

    点评 本题考查的是翻折变换的性质和三角形内角和定理，找准翻折变换中相等的角是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．列方程或方程组解应用题：
    为打造刺猬河沿岸的风光带，有一段长为360米的河道整治任务由A、B两个工程队先后接力完成．A工程队每天整治24米，B工程队每天整治16米，共用时20天．
    （1）根据题意，甲、乙两个同学分别列出了尚不完整的方程组如下：
    甲：$\left\{\begin{array}{l}x+y=\\ \\ 24x+16y=\end{array}\right.$乙：$\left\{\begin{array}{l}x+y=\\ \frac{x}{24}+\frac{y}{16}=\end{array}\right.$
    根据甲、乙两名同学所列的方程组，请你分别指出未知数x，y表示的意义，并且在方框中补全甲、乙两名同学所列的方程组：
    甲：x表示A队的工作时间，y表示B队的工作时间；
    乙：x表示A队的工作量，y表示B队的工作量．
    （2）求出其中一个方程组的解，并回答A、B两工程队分别整治河道多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

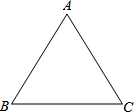    4．如图，在等边三角形ABC的每个顶点处均有一只蚂蚁，这三只蚂蚁同时出发，以相同的速度在等边三角形ABC的三边上匀速爬行，请你求出它们都不相遇的概率？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．使$\sqrt{6-2x}$有意义的x的取值范围是x≤3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．用描点法作出函数y=$\left\{\begin{array}{l}{2x（0≤x≤3）}\\{3x-3（x＞3）}\end{array}\right.$的图象，并求当y=36时，x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

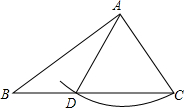    18．学习了全等三角形后，同学们都知道存在“边角边”的判定方怯．接着同学们探究是否存在“边边角”的判定方法，即“有两边和其中一边的对角对应相等的两个三角形全等”这个命题是真命题还是假命题．
    小明给出了反例：如图，在△ABC和△ABD中，已知两边AB=AB，AC=AD及AC，AD的对角∠B=∠B，但△ABC是锐角三角形，△ABD是钝角三角形，显然不全等．这个反例说明用”边边角”不能判定两个三角形全等．
    （1）探究过程中，小亮提出问题：“如果符合条件的两个三角形都是直角三角形，那这两个三角形是否全等呢？”请你回答“有两边及其中一边的对角对应相等的两个直角三角形全等”是真命题（填“真命题”或“假命题”）．
    （2）小兵认为“两边及其中一边的对角对应相等的两个锐角三角形全等”是真命题，请你帮他证明．（画出图形，写出已知求证并证明）．
    （3）“两边及其中一边的对角对应相等的两个钝角三角形全等”是真命题还是假命题？如果是真命题，请画出图形，写出已知求证并证明，如果是假命题，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某校为提高教师业务素质，开展了“课内比教学”为主题的讲课比赛，比赛设一个第一名，一个第二名，两个并列第三名．前四名中七、八年级各有一名教师，九年级有两名教师，分管九年级的林校长认为前两名是九年级教师的概率是$\frac{1}{2}$，你赞成他的观点吗？请用列表法或画树形图法分析说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如果$\frac{a}{2x+3y}$+$\frac{b}{2x-3y}$=$\frac{4x}{4{x}^{2}-9{y}^{2}}$，那么a=1，b=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：（-1×$\frac{1}{2}$）+（$-\frac{1}{2}×\frac{1}{3}$）+（$-\frac{1}{3}×\frac{1}{4}$）+…+（$-\frac{1}{2013}×\frac{1}{2014}$）+（$-\frac{1}{2014}×\frac{1}{2015}$）．

    查看答案和解析>>

    同步练习册答案