
【题目】如图,已知![]() 半径为
半径为![]() ,弦
,弦![]() 垂直平分半径
垂直平分半径![]() ,并交
,并交![]() 于点
于点![]() .
.
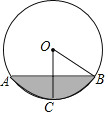
(1)求弦![]() 的长;
的长;
(2)求弧![]() 的长,并求出图中阴影部分面积.
的长,并求出图中阴影部分面积.
【答案】(1)10![]() cm;(2)
cm;(2)![]() cm,
cm,![]() cm2.
cm2.
【解析】
(1)先利用垂径定理得出AB=2BD,∠ODB=90°,OD=![]() OC=5,进而根据勾股定理求出BD,即可得出结论;
OC=5,进而根据勾股定理求出BD,即可得出结论;
(2)先利用锐角三角函数求出∠BOD=60°,最后利用扇形的弧长公式和扇形的面积公式即可得出结论.
(1)如图,⊙O半径为10cm,
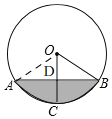
∴OB=OC=10,
∵弦AB垂直平分半径OC,
∴AB=2BD,∠ODB=90°,OD=![]() OC=5,
OC=5,
在Rt△BOD中,根据勾股定理得,BD=![]() ,
,
∴AB=2BD=10![]() cm;
cm;
(2)由(1)知,OD=5,
在Rt△BOD中,cos∠BOD=![]() ,
,
∴∠BOD=60°,
∵OC⊥AB,
∴∠AOB=2∠BOD=120°,
∴弧![]() cm,
cm,
S阴影=S扇形AOB-S△AOB=![]() (cm2).
(cm2).


科目:初中数学 来源: 题型:
【题目】(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
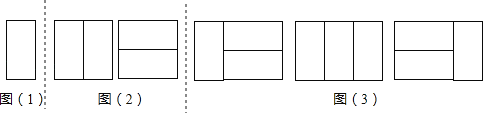
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?
一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?
(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1,an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 种不同的镶嵌方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
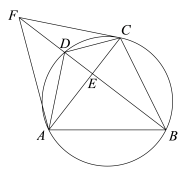
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 为常数)交
为常数)交![]() 轴于点
轴于点![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,顶点为
之间,顶点为![]() .
.
①抛物线![]() 与直线
与直线![]() 有且只有一个交点;
有且只有一个交点;
②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]()
③将该抛物线向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位,所得抛物线解析式为
个单位,所得抛物线解析式为![]() ;
;
④点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() 点
点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中正确判断的序号是( )
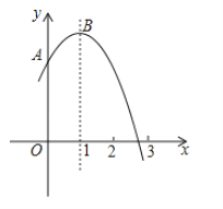
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() 为
为![]() 内一点,将
内一点,将![]() 绕点
绕点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() 得到
得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,且
,且![]() 三点在同一直线上.
三点在同一直线上.
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)如图2,若![]() ,请补全图形,再过点
,请补全图形,再过点![]() 作
作![]() 于点
于点![]() ,然后探究线段
,然后探究线段![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)若![]() ,且点
,且点![]() 满足
满足![]() ,直接写出点
,直接写出点![]() 到
到![]() 的距离.
的距离.
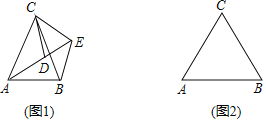
查看答案和解析>>
科目:初中数学 来源: 题型:
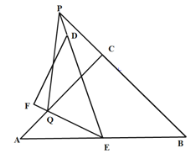
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠ACB=∠EFD=90,△DEF,的顶点E与△ABC的斜边AB的中点重合.将△DEF绕点E旋转,旋转过程中,线段AC与线段EF相交于点Q,射线ED与射线BC相交于点P.
(1)求证:△AEQ∽△BPE;
(2)求证:PE平分∠BPQ;
(3)当AQ=2,AE=![]() ,求PQ的长.
,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一枚均匀的正四面体,四个面上分别标有数字1,2,3,4,小红随机地抛掷一次,把着地一面的数字记为x;另有三张背面完全相同,正面上分别写有数字-2,-1,1的卡片,小亮将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后他们计算出S=x+y的值.
(1)用树状图或列表法表示出S的所有可能情况;
(2)分别求出当S=0和S<2时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com