
【题目】如图,已知:![]() 都是等边三角形,
都是等边三角形,![]() 与
与![]() 相交于点
相交于点![]() .
.
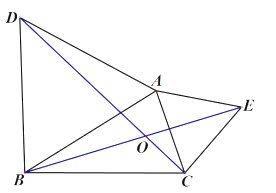
![]() 求
求![]() 的度数?
的度数?
![]() 探究
探究![]() 满足怎样条件时?
满足怎样条件时?![]() 与
与![]() 互相平分,并说明理由.
互相平分,并说明理由.
【答案】![]() ;
;![]() 且
且![]() ,理由见解析.
,理由见解析.
【解析】
(1)先证得∠BAE=∠DAC,然后根据已知条件即可证得△ABE≌△ADC,所以∠ABE=∠ADC,所以∠AFD=∠OFB,根据三角形的内角和得出∠BOD=∠DAB=60°,所以![]()
(2)先猜想出:![]() 且
且![]() 时,
时,![]() 与
与![]() 互相平分.再理由猜想条件与已知条件证明四边形
互相平分.再理由猜想条件与已知条件证明四边形![]() 是平行四边形即可.
是平行四边形即可.
(1)证明:∵∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠BAE=∠DAC,
在△BAE与△DAC中,
 ,
,
∴△ABE≌△ADC(SAS),
∴∠ABE=∠ADC,
设![]() 与DC相交于F,
与DC相交于F,
∴∠AFD=![]() ,
,
∴∠![]() =∠DAB=60°,
=∠DAB=60°,
∴![]() =120°;
=120°;
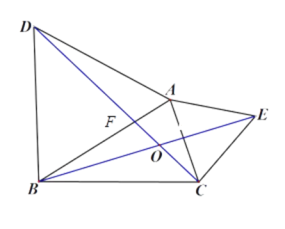
(2)猜想:![]() 且
且![]() 时,
时,![]() 与
与![]() 互相平分.
互相平分.
理由如下:
![]()
![]()
![]() 为等边三角形,
为等边三角形,
![]()
![]()
![]()
![]()
![]() 为等边三角形,
为等边三角形,![]()
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 与
与![]() 互相平分.
互相平分.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
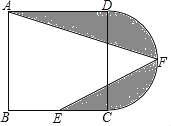
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在疫情期间用3000元购进A、B两种口罩1100个,购买A种口罩与购买B种口罩的费用相同,且A种口罩的单价是B种口罩单价的1.2倍;
(1)求A,B两种口罩的单价各是多少元?
(2)若计划用不超过7000元的资金再次购进A、B两种口罩共2600个,已知A、B两种口罩的进价不变,求A种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) | … | 5 | 10 | 15 | 20 | … |
y(元/件) | … | 75 | 70 | 65 | 60 | … |
(1)由题意知商品的最低销售单价是 元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
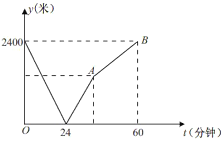
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离y (米)与时间t (分钟)之间的函数关系如图所示,根据图象信息知,点A的坐标是__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
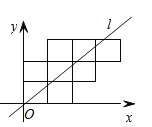
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线![]() 将这八个正方形分成面积相等的两部分,则该直线
将这八个正方形分成面积相等的两部分,则该直线![]() 的解析式为( )
的解析式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com