
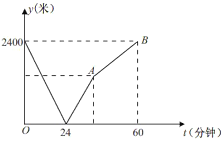
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离y (米)与时间t (分钟)之间的函数关系如图所示,根据图象信息知,点A的坐标是__________;
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.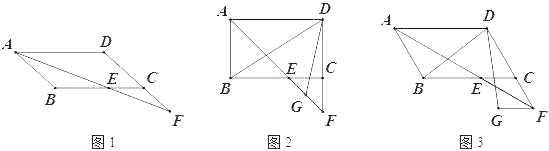
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°

(1)利用尺规作∠ABC 的平分线,交AC 于点O,再以O 为圆心,OC 的长为半径作⊙O(保留作图痕迹,不写作法);
(2)在你所作的图中,①判断AB 与⊙O 的位置关系,并证明你的结论;②若AC=12,tan∠OBC=![]() ,求⊙O 的半径。
,求⊙O 的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
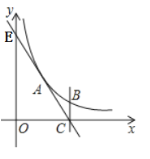
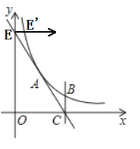
【题目】如图,反比例函数y=![]() (x>0) 过点A (3,4),直线AC与x轴交于点C (6,0),交y轴于点E,过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0) 过点A (3,4),直线AC与x轴交于点C (6,0),交y轴于点E,过点C作x轴的垂线BC交反比例函数图象于点B.
(1)求k的值与B点的坐标;
(2)将直线EC向右平移,当点E正好落在反比例函数图象上的点E' 时,直线交x轴于点F.请判断点B是否在直线EF上并说明理由;
(3)在平面内有点M,使得以A、B、F、M四点为顶点的四边形为平行四边形,请直接写出符合条件的所有M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
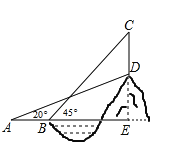
【题目】某数学课外兴趣小组为了测量池塘对岸山丘![]() 上的塔
上的塔![]() 的高度,在山脚下的广场
的高度,在山脚下的广场![]() 处测得建筑物点
处测得建筑物点![]() (即山顶)的抑角为
(即山顶)的抑角为![]() ,沿水平方向前进245米到达
,沿水平方向前进245米到达![]() 点,测得建筑物顶部
点,测得建筑物顶部![]() 点的仰角为
点的仰角为![]() ,已知山丘
,已知山丘![]() 高182米,求塔
高182米,求塔![]() 的高度.(结果精确到0.1米,参考数据
的高度.(结果精确到0.1米,参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
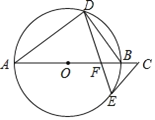
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径长为5,BF=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数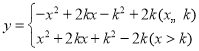 ,(
,(![]() 为常数).
为常数).
(1)当![]() 时,
时,
①求此函数图象与![]() 轴交点坐标.
轴交点坐标.
②当函数![]() 的值随
的值随![]() 的增大而增大时,自变量
的增大而增大时,自变量![]() 的取值范围为________.
的取值范围为________.
(2)若已知函数经过点(1,5),求![]() 的值,并直接写出当
的值,并直接写出当![]() 时函数
时函数![]() 的取值范围.
的取值范围.
(3)要使已知函数![]() 的取值范围内同时含有
的取值范围内同时含有![]() 和
和![]() 这四个值,直接写出
这四个值,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com