
【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
【答案】⑴ x≠0;⑵ -1,3,详见解析;⑶ 小,3 ;⑷ a≥1
【解析】
(1)根据分式的分母不能为0即可得;
(2)分别将![]() 和
和![]() 代入函数的解析式可求出对应的y的值,再利用描点法画出这个函数的大致图象即可;
代入函数的解析式可求出对应的y的值,再利用描点法画出这个函数的大致图象即可;
(3)根据算术—几何均值不等式求解即可得;
(4)根据(2)所画出的函数图象得出y随x增大而增大时,x的取值范围,由此即可得出答案.
(1)由分式的分母不能为0得:函数![]() 的自变量x的取值范围是
的自变量x的取值范围是![]()
故答案为:![]() ;
;
(2)对于函数![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
因此,补全表格如下:
x | … |
|
|
|
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
|
| 3 | 5 |
| … |
利用描点法画出这个函数的大致图象如下:

(3)函数![]() 在第一象限时,
在第一象限时,![]()
由算术—几何均值不等式得:![]()
则![]() 有最小值,最小值为3
有最小值,最小值为3
故答案为:小,3;
(4)由(2)的函数图象可知,当![]() 时,y随x增大而增大
时,y随x增大而增大
则a的取值范围是![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
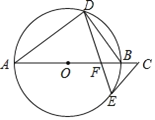
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径长为5,BF=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解一批灯泡的使用寿命采用全面调查
B.一组数据6,5,3,5,4的众数是5,中位数是3
C.“367人中必有2人的生日是同一天”是必然事件
D.一组数据10,11,12,9,8的平均数是10,方差是1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,过
,过![]() 点的直线
点的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线
,与抛物线![]() 的另一个交点为
的另一个交点为![]() ,己知
,己知![]() ,
,![]() ,
,![]() 点为抛物线
点为抛物线![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).
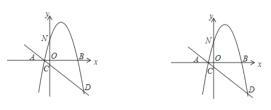
(1)直接写出抛物线和直线![]() 的解析式;
的解析式;
(2)当点![]() 在直线
在直线![]() 上方的抛物线上时,连接
上方的抛物线上时,连接![]() 、
、![]() ,
,
①当![]() 的面积最大时,
的面积最大时,![]() 点的坐标是________;
点的坐标是________;
②当![]() 平分
平分![]() 时,求线段
时,求线段![]() 的长.
的长.
(3)设![]() 为直线
为直线![]() 上的点,探究是否存在点
上的点,探究是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() ,
,![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,直接写出点
为顶点的四边形为平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
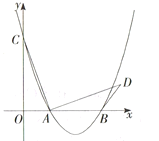
【题目】如图,在平面直角坐标系中,抛物线![]() (
(![]() 是常数,且
是常数,且![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() .连结
.连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() .当
.当![]() 最短时,
最短时,![]() 的值为_________ .
的值为_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数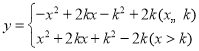 ,(
,(![]() 为常数).
为常数).
(1)当![]() 时,
时,
①求此函数图象与![]() 轴交点坐标.
轴交点坐标.
②当函数![]() 的值随
的值随![]() 的增大而增大时,自变量
的增大而增大时,自变量![]() 的取值范围为________.
的取值范围为________.
(2)若已知函数经过点(1,5),求![]() 的值,并直接写出当
的值,并直接写出当![]() 时函数
时函数![]() 的取值范围.
的取值范围.
(3)要使已知函数![]() 的取值范围内同时含有
的取值范围内同时含有![]() 和
和![]() 这四个值,直接写出
这四个值,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (
(![]() )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③![]() ;
;
④![]() ;
;
其中正确的结论是( )

A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
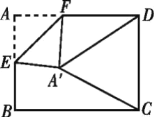
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 所在直线翻折,得到
所在直线翻折,得到![]() ,连接
,连接![]() ,
,![]() ,则当
,则当![]() 是以
是以![]() 为腰的等腰三角形时,
为腰的等腰三角形时,![]() 的长是___________.
的长是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com