
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 所在直线翻折,得到
所在直线翻折,得到![]() ,连接
,连接![]() ,
,![]() ,则当
,则当![]() 是以
是以![]() 为腰的等腰三角形时,
为腰的等腰三角形时,![]() 的长是___________.
的长是___________.
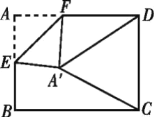
【答案】![]() 或
或![]()
【解析】
题干仅告知了![]() 是以
是以![]() 为腰的等腰三角形,存在两种情况,一种是
为腰的等腰三角形,存在两种情况,一种是![]() ,连接ED,利用勾股定理求ED的长,可判断点E、
,连接ED,利用勾股定理求ED的长,可判断点E、![]() 、D三点共线,最后在Rt△F
、D三点共线,最后在Rt△F![]() D中可求得;另一种情况是
D中可求得;另一种情况是![]() ,证四边形AE
,证四边形AE![]() F是正方形,可求得.
F是正方形,可求得.
情况一:当![]() 时,如下图,连接ED
时,如下图,连接ED
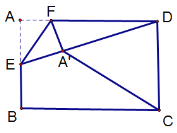
∵点E是AB的中点,AB=4,![]() ,四边形ABCD是矩形
,四边形ABCD是矩形
∴AD=![]() ,∠A=90°
,∠A=90°
∴在Rt△ADE中,ED=6
∵将![]() 沿
沿![]() 所在直线翻折,得到
所在直线翻折,得到![]()
∴![]() =AE=2
=AE=2
∵![]() =AB=4
=AB=4
∴ED=![]() +
+![]()
∴点E、![]() 、D三点共线
、D三点共线
∵∠A=90°
∴∠F![]() E=∠F
E=∠F![]() D=90°
D=90°
设AF=x,则![]() F=x,FD=
F=x,FD=![]() -x
-x
∴在Rt△F![]() D中,
D中,![]() ,解得:x=
,解得:x=![]()
∴FD=3![]()
情况二:当![]() 时,如下图
时,如下图
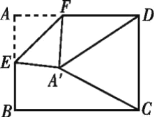
∵![]()
∴点![]() 在线段CD的垂直平分线上
在线段CD的垂直平分线上
∴点![]() 在线段AB的垂直平分线上
在线段AB的垂直平分线上
∵点E是AB的中点
∴E![]() 是AB的垂直平分线
是AB的垂直平分线
∴∠AE![]() =90°
=90°
∵将![]() 沿
沿![]() 所在直线翻折,得到
所在直线翻折,得到![]() ,四边形ABCD是矩形
,四边形ABCD是矩形
∴∠A=∠E![]() F=90°,AF=F
F=90°,AF=F![]()
∴四边形AE![]() F是正方形
F是正方形
∴AF=AE=2
∴FD=![]()
故答案为:![]() 或
或![]()


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC交AC于点E,AC的反向延长线交⊙O于点F.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠C=30°,⊙O的半径为6,求弓形AF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
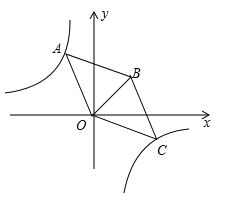
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 为坐标原点,且与反比例函数
为坐标原点,且与反比例函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,且
两点,且![]() 点的纵坐标为
点的纵坐标为![]() ,已知点
,已知点![]() ,则
,则![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.9D.
C.9D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:
已知:![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,将线段
,将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .当点
.当点![]() 在如图所示的位置时:
在如图所示的位置时:
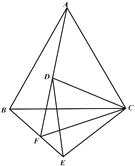
(1)观察填空:
①与![]() 全等的三角形是________;
全等的三角形是________;
②![]() 的度数为
的度数为
(2)利用题干中的结论,证明:![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.____________________.
之间的数量关系.____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
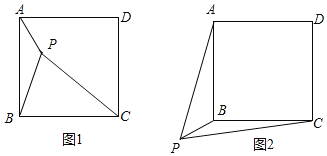
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
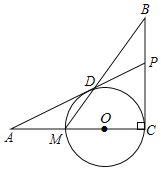
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是⊙O的切线;
(3)若AD=12,AM=MC,求PB和DM的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com