
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于
的延长线于![]() .
.
(1)若![]() ,
,![]() 的长;
的长;
(2)求证:![]() .
.
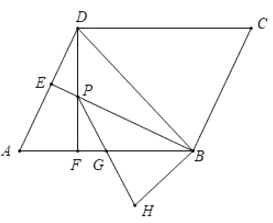
【答案】(1)DP=![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)过P作PM⊥BD于M,根据角平分线的性质得PM=PF,证明Rt△BFP≌R△BMP(HL),得BM=BF=![]() ,求出DM=
,求出DM=![]() ,根据等腰直角三角形的性质可得结论;
,根据等腰直角三角形的性质可得结论;
(2)连接AP,构建全等三角形,先证明△ADF≌△PBF(ASA),得PF=AF,再证明△APG≌△BHG(ASA),得BH=AP,求出∠ADP=∠DAP=22.5°得AP=DP,从而得结论.
解:(1)如图,过P作PM⊥BD于M,
∵四边形ABCD是平行四边形,
∴CD=AB=BD=4,
∵E是AD的中点,
∴∠DBE=∠ABE,
∵PF⊥AB,PM⊥BD,
∴PF=PM,
∵∠ABD=45°,
∴△BDF是等腰直角三角形,
∴DF=BF=![]() ,∠BDF=45°,
,∠BDF=45°,
∴DM=PM,PD=![]() DM,
DM,
在Rt△BFP和Rt△BMP中,
∵PF=PM,BP=BP,
∴Rt△BFP≌Rt△BMP(HL),
∴BM=BF=![]() ,
,
∴DM=![]() ,
,
∴DP=![]() DM=
DM=![]() ;
;
(2)连接AP,
∵∠DEP=∠PFB=90°,∠EPD=∠FPB,
∴∠EDP=∠FBP,
又∵DF=BF,∠AFD=∠BFP=90°,
∴△ADF≌△PBF(ASA),
∴PF=AF,
∴∠PAF=45°,
∵BD⊥BH,
∴∠DBH=90°,
∵∠DBF=45°,
∴∠HBG=90°45°=45°,
∴∠PAF=∠HBG,
又∵AG=BG,∠PGA=∠HGB,
∴△APG≌△BHG(ASA),
∴BH=AP,
∵AB=BD,∠ABD=45°,
∴∠DAB=∠ADB=67.5°,
∴∠ADP=∠DAP=22.5°,
∴AP=DP,
∴![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,过
,过![]() 点的直线
点的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线
,与抛物线![]() 的另一个交点为
的另一个交点为![]() ,己知
,己知![]() ,
,![]() ,
,![]() 点为抛物线
点为抛物线![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).
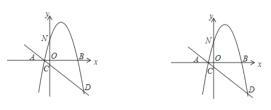
(1)直接写出抛物线和直线![]() 的解析式;
的解析式;
(2)当点![]() 在直线
在直线![]() 上方的抛物线上时,连接
上方的抛物线上时,连接![]() 、
、![]() ,
,
①当![]() 的面积最大时,
的面积最大时,![]() 点的坐标是________;
点的坐标是________;
②当![]() 平分
平分![]() 时,求线段
时,求线段![]() 的长.
的长.
(3)设![]() 为直线
为直线![]() 上的点,探究是否存在点
上的点,探究是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() ,
,![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,直接写出点
为顶点的四边形为平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中∠A=∠ABC=90°,点E是CD的中点,△ABD与 △EBD关于直线BD对称,![]() ,
,![]() .
.
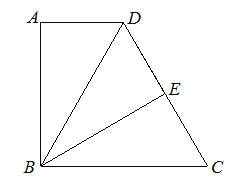
(1)求点A和点E之间的距离;
(2)联结AC交BE于点F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
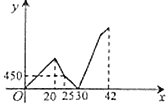
【题目】小杰早上从家匀速步行去学校,走到途中发现英语书忘在家里了,随即打电话给爸爸,爸爸立即送英语书去,小杰掉头以原速往回走,几分钟后,路过一家文具店,此时还未遇到爸爸,小杰便在文具店购买了几个笔记本,刚付完款,爸爸刚好赶到,将英语书交给了小杰(途中小杰打电话、小杰的爸爸找英语书的时间忽略不计):然后,爸爸原速返回,同时小杰把速度提高到原来的![]() 前往学校,爸爸到家后,过一会小杰才到达学校.两人之间的距离
前往学校,爸爸到家后,过一会小杰才到达学校.两人之间的距离![]() (米)与小杰从家出发的时间
(米)与小杰从家出发的时间![]() (分钟)的函数关系如图所示,则家与学校相距______米.
(分钟)的函数关系如图所示,则家与学校相距______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 所在直线翻折,得到
所在直线翻折,得到![]() ,连接
,连接![]() ,
,![]() ,则当
,则当![]() 是以
是以![]() 为腰的等腰三角形时,
为腰的等腰三角形时,![]() 的长是___________.
的长是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )
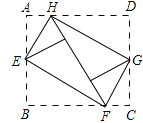
A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
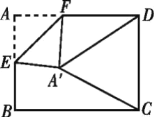
【题目】如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为 ___________cm2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
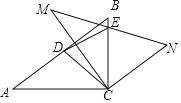
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=8,BC=6,将△ABC绕点C顺时针旋转得到△MCN,点D、E分别为AB、MN的中点,若点E刚好落在边BC上,则sin∠DEC=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com