
分析 (1)原式变形后,提取公因式即可得到结果;
(2)原式变形后,提取公因式即可得到结果;
(3)原式提取公因式即可得到结果;
(4)原式提取公因式即可得到结果;
(5)原式变形后,提取公因式即可得到结果;
(6)原式变形后,提取公因式即可得到结果;
(7)原式变形后,提取公因式即可得到结果;
(8)原式变形后,提取公因式即可得到结果.
解答 解:(1)原式=3x(x-2)+(x-2)=(x-2)(3x+1);
(2)原式=-4q(p-1)3+2(p-1)2=2(p-1)2(-2qp+2q+1);
(3)原式=-2mn(-2mn-6m2n+1);
(4)原式=axn-1(ax3+bx2-cx-d);
(5)原式=a(a-b)2(a-b+2a2-2ab);
(6)原式=3x(a-b)(ay-by-9x);
(7)原式=(2x-1)y[y-(2x-1)2];
(8)原式=a(a-1)2(a-1)=a(a-1)3.
点评 此题考查了提公因式与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
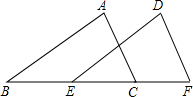 △ABC≌△DEF,AC与DF是对应边,∠A与∠D是对应角.
△ABC≌△DEF,AC与DF是对应边,∠A与∠D是对应角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com