
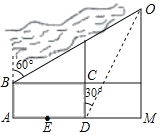
����Ŀ����ͼ��ʾ��С�����ڵ�O����������ѧУ��УΪ����ABCD��������AD��1000�ף��ϱ���AB��600�ף�ѧУ����������AD���е�E����BΪѧУ���������ţ�С���Ӽҵ�ѧУ��������·��·��O��M��E����M��90������Ҳ�������غӹ۹�·��·��O��B��С����D�����Oλ�ڱ�ƫ��30������B�����Oλ�ڱ�ƫ��60��С���Ӽҵ�ѧУ������·���У���·�߱ȶ�·�߶�_____�ף�������������ţ�
���𰸡�![]()
��������
��ͼ��������ã���OBF��30����DOM��30����FM��AB��600����DM��CF��x���õ�BF��1000+x����ֱ�������μ��ɵõ����ۣ�
�⣺��ͼ��������ã���OBF��30����DOM��30����FM��AB��600��
��DM��CF��x��
��BF��1000+x��
��Rt��BOF�У��ߡ�OBF��30����
��OF��![]() BF��
BF��![]() ��OB��
��OB�� ��
��
��Rt��ODM��DM��x��
��OM��![]() x��
x��
��OF��OM��FM��![]() x��600��
x��600��
��![]() ��
��![]() x��600��
x��600��
��ã�x��500+300![]() ��
��
��OF��500![]() +300��
+300��
��BO��2OF��1000![]() +600��
+600��
��·��O��M��E�ij��ȣ�500+x+![]() x��500+500+300
x��500+500+300![]() +500
+500![]() +900��1900+800
+900��1900+800![]() ��
��
�·�߱ȶ�·�߶ࣨ1300��200![]() ���ף�
���ף�
�ʴ�Ϊ��1300��200![]() ��
��



 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
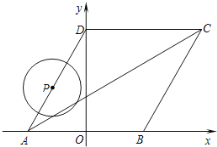
����Ŀ����ͼ��ʾ������ABCD�Ķ���A��B��![]() ���ϣ���A�ڵ�B����࣬��D��
���ϣ���A�ڵ�B����࣬��D��![]() ����������ϣ�
����������ϣ�![]() ����A������Ϊ
����A������Ϊ![]() .
.
(1)��D�������.
(2)��ֱ��AC�ĺ�����ϵʽ.
(3)����P�ӵ�A��������ÿ��1����λ���ȵ��ٶȣ�����![]() ��˳�������εı��������˶�һ�ܣ����˶�ʱ��Ϊ
��˳�������εı��������˶�һ�ܣ����˶�ʱ��Ϊ![]() ��.��
��.��![]() Ϊ��ֵʱ���Ե�PΪԲ�ġ���1Ϊ�뾶��Բ��Խ���AC���У�
Ϊ��ֵʱ���Ե�PΪԲ�ġ���1Ϊ�뾶��Բ��Խ���AC���У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬D��![]() ���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE��2��C��AC��BD���ڵ�H����OE���ڵ�F��
���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE��2��C��AC��BD���ڵ�H����OE���ڵ�F��
��1����֤��AE�ǡ�O�����ߣ�
��2����DH��9��tanC��![]() ����ֱ��AB�ij���
����ֱ��AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����ADE���ǵ���ֱ�������Σ���ACB=��ADE=90������FΪBE���е㣬����CF��DF��

��1����ͼ1������D��AB�ϣ���E��AC��ʱ
��֤������BFC�ǵ��������Σ�
�����ж��߶�CF��DF�Ĺ�ϵ����˵�����ɣ�
��2����ͼ2����ͼ1�е���ADE�Ƶ�A��ת��ͼ2λ��ʱ�����жϣ�1���ТڵĽ����Ƿ���Ȼ��������֤������жϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
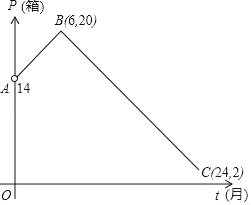
����Ŀ��ij����Ʒ�ӹ��������г����н�����Ըó�������һ����������Ʒ���δ����������۽���Ԥ�⣬����������ģ�ͣ����t���£�����Ʒ������ΪP����λ���䣩��P��t֮�������ͼ��ʾ������ϵ����ͼ�����߶�AB��������A�����߶�BC����ϣ����t��������ÿ���ë����ΪQ����Ԫ������Q��t�������¹�ϵQ=2t+8��0��t��24����
��1����P��t�ĺ�����ϵʽ��6��t��24����
��2���ó��ڵڼ������ܹ�������ë�������ë�����Ƕ��٣�
��3�������鷢�֣�����ë������40000�Ҳ�����43200Ԫʱ�����²�Ʒԭ���Ϲ������г������г����ʱ�������Ϊ����г��������ô����δ�������еڼ�����Ϊ��г�£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�½���վվǰ�㳡��Ҫ�̻������Ϊ46000��2��ʩ�������̻���22000��2��ÿ��Ĺ���������Ϊԭ����1.5���������ǰ4������˸����̻����̣�
��1�������̻�����ԭ�ƻ�ÿ����ɶ�����2��
��2�������̻���������һ�鳤Ϊ20�ף���Ϊ8�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ56��2�������̵�֮�估�ܱ����п�����ȵ�����ͨ������ͼ��ʾ����������ͨ���Ŀ����Ƕ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ��Ӫ����Ƿ��68400Ԫ����Ϣ�����ծ����ת�о�Ӫ��װר������ȱ���ʽ𣮡��й������㡱��Ŀ���������õ�30000Ԫ�ʽ𣬲�Լ�����þ�Ӫ������ծ������ծ���������Ϣ������֪�õ������Ʒ�Ʒ�װ�Ľ���Ϊÿ��40Ԫ����Ʒ�Ʒ�װ��������![]() �����������ۼ�
�����������ۼ�![]() ��Ԫ����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ�����ʾ���õ�Ӧ֧��Ա���Ĺ���Ϊÿ��ÿ��82Ԫ��ÿ�컹Ӧ֧����������Ϊ106Ԫ��������ծ��
��Ԫ����֮��Ĺ�ϵ����ͼ�е�һ�����ߣ�ʵ�ߣ�����ʾ���õ�Ӧ֧��Ա���Ĺ���Ϊÿ��ÿ��82Ԫ��ÿ�컹Ӧ֧����������Ϊ106Ԫ��������ծ��
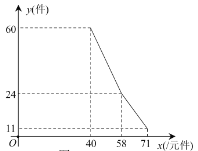
��1������������![]() �����������ۼ�
�����������ۼ�![]() ��Ԫ/����֮��ĺ�����ϵʽ��
��Ԫ/����֮��ĺ�����ϵʽ��
��2�����õ��ݲ����dz���ծ��ij������ۼ�Ϊ48Ԫ/��ʱ������������֧ƽ�⣨����=֧��������õ�Ա����������
��3�����õ�ֻ��2��Ա������õ�������Ҫ�������ܻ�������ծ��ʱÿ����װ�ļ۸�Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
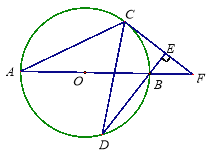
����Ŀ����ͼ��ABΪ��Oֱ����C��DΪ��O����ͬ��A��B����������ABD=2��BAC������CD.����C��CE��DB������ΪE��ֱ��AB��CE�ཻ��F��.
��1����֤��CFΪ��O��������
��2����BF=5,![]() ʱ����BD�ij�.
ʱ����BD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
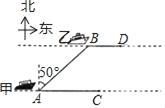
����Ŀ����ͼ�������ϼס��������ֱ��A��B����ͬʱ��������������ʻ���״����ٶ�Ϊ24n mile/h���Ҵ����ٶ�Ϊ15n mile/h������ʱ������Ҵ��ڼ״���ƫ��50�㷽����AB=10nmile������20���Ӻס��������ֱ�C��D������
���ο�ֵ��sin50����0.766��cos50���0.643��tan50���1.192��
��1������������ľ��룻
��2������������ԭ�����ٶȺͺ�����Ҫ����ʱ�����ʹ�����ľ�����̣�����ȷ��0.01��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com