【题目】如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )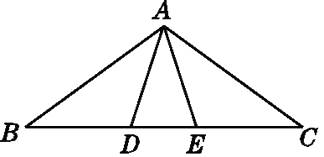
A.3个
B.4个
C.5个
D.6个
【答案】D
【解析】解：∵∠B=∠C=36°，∠ADE=∠AED=72°，∴△ABC和△ADE是等腰三角形，
∵∠B=36°，∠ADE=72°，
∴∠BAD=36°，
∴△ABD是等腰三角形，同理△AEC是等腰三角形，
∵∠ADE=∠AED=72°，
∴∠DAE=36°，
∴∠CAD=36°+36°=72°，
∴∠CAD=∠CDA=72°，
∴△ADC是等腰三角形，
同理：△ABE是等腰三角形，
综上所述：等腰三角形有6个，
故应选：D 。
根据有两个内角相等的三角形是等腰三角形得出△ABC和△ADE是等腰三角形；根据三角行的外角定理得出∠BAD=36°=∠B,从而得出△ABD是等腰三角形，同理△AEC是等腰三角形；根据三角形的内角和得出∠DAE=36°，根据角的和差得出∠CAD=36°+36°=72°，进而得出∠CAD=∠CDA=72°，故△ADC是等腰三角形，同理：△ABE是等腰三角形；从而得出结论。
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，对于平面内任意一点（x，y），若规定以下两种变换：
①f（x，y）＝（x+2，y），
②g（x，y）＝（﹣x，﹣y），例如按照以上变换有：f（1，1）＝（3，1）；g（f（1，1））＝g（3，1）＝（﹣3，﹣1）．
则f（g（2，5））＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）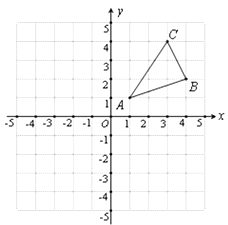
⑴ 作出与△ABC关于y轴对称△A1B1C1 ， 并写出三个顶点的坐标为：A1（），B1（），C1（）；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=
交于A（1，3）和B（﹣3，﹣1）两点．
观察图象可知：
①当x=﹣3或1时，y1=y2；
②当﹣3＜x＜0或x＞1时，y1＞y2，即通过观察函数的图象，可以得到不等式ax+b＞
的解集．
有这样一个问题：求不等式x3+4x2﹣x﹣4＞0的解集．
某同学根据学习以上知识的经验，对求不等式x3+4x2﹣x﹣4＞0的解集进行了探究．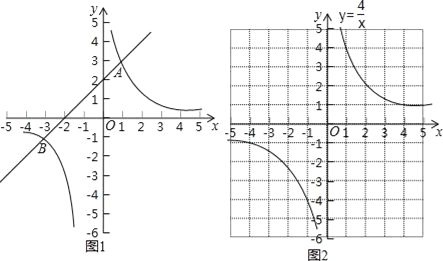
下面是他的探究过程，请将（2）、（3）、（4）补充完整：
（1）将不等式按条件进行转化：
当x=0时，原不等式不成立；
当x＞0时，原不等式可以转化为x2+4x﹣1＞
；
当x＜0时，原不等式可以转化为x2+4x﹣1＜
；
（2）构造函数，画出图象
设y3=x2+4x﹣1，y4=
，在同一坐标系中分别画出这两个函数的图象．
双曲线y4=
如图2所示，请在此坐标系中画出抛物线y3=x2+4x﹣1；（不用列表）
（3）确定两个函数图象公共点的横坐标
观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为 ；
（4）借助图象，写出解集
结合（1）的讨论结果，观察两个函数的图象可知：不等式x3+4x2﹣x﹣4＞0的解集为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
