
| 价格 品种 地区 | 黄帝蕉 (元/千克) | 香牙蕉 (元/千克) |
| 海口 | 5 | 4.8 |
| 文昌 | 4.2 | 3.6 |
分析 (1)设种植园供应海口市的黄帝蕉是x千克,则供应海口市的香牙蕉是2x千克,根据等量关系:种植园供应海口市的黄帝蕉质量+种植园供应海口市的香牙蕉质量=15000千克,列出方程求得x,进一步得到该种植园供应文昌市的香牙蕉与黄帝蕉各是多少千克;
(2)设应安排m千克香牙蕉在海口市销售,则在海口市销售的黄帝蕉为(15000-m)千克;在文昌市销售的香牙蕉与黄帝蕉分别为(12000-m)千克、(m-7000)千克,根据总价=单价×数量可求这批香蕉的销售收入y与m的函数关系式为y=0.4m+88800 (7000≤m≤12000),从函数关系式看m的值越大,销售收入y就越大,即香牙蕉应尽可能多地安排在海口市销售,所以若要使销售收入最大,需安排12000千克香牙蕉与3000千克黄帝蕉在海口市卖,安排5000千克黄帝蕉在文昌市卖,从而得到最大销售收入.
解答 解:(1)设种植园供应海口市的黄帝蕉是x千克,则供应海口市的香牙蕉是2x千克,根据题意列方程得:
2x+x=15000,
解得:x=5000,
则2x=10000,
则种植园供应文昌市的香牙蕉是12000-10000=2000千克,
种植园供应文昌市的黄帝蕉是5000-2000=3000千克.
答:种植园供应文昌市的香牙蕉是2000千克,种植园供应文昌市的黄帝蕉是3000千克.
(2)设应安排m千克香牙蕉在海口市销售,则在海口市销售的黄帝蕉为(15000-m)千克;
在文昌市销售的香牙蕉与黄帝蕉分别为(12000-m)千克、(m-7000)千克,
则这批香蕉的销售收入y与m的函数关系式为:y=4.8m+5(15000-m)+3.6(12000-m)+4.2(m-7000),
即y=0.4m+88800 (7000≤m≤12000),
从函数关系式看m的值越大,销售收入y就越大,即香牙蕉应尽可能多地安排在海口市销售,
所以若要使销售收入最大,需安排12000千克香牙蕉与3000千克黄帝蕉在海口市卖,
安排5000千克黄帝蕉在文昌市卖,最大销售收入为y=0.4×12000+88800=93600(元).
点评 此题考查了应用类问题,综合性较强,难度较大,解答本题的关键是认真审题,将实际问题转化为数学问题解答.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
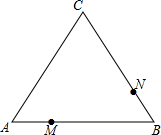 如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.
如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
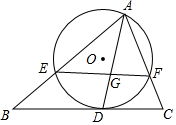 如图,⊙O为△AEF的外接圆,BC与⊙O相切于点D,交AE,AF的延长线于点B,C.AD平分∠BAC,EF交AD于点G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.
如图,⊙O为△AEF的外接圆,BC与⊙O相切于点D,交AE,AF的延长线于点B,C.AD平分∠BAC,EF交AD于点G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com