
【题目】(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.

【答案】(1)作图见解析;(2)证明见解析;(3)m=![]() .
.
【解析】
试题本题主要考查的是一次函数的图象和性质,掌握一次函数的图象和性质是解题的关键.
(1)将函数y=|x|,变形为y=x(x≥0),y=﹣x(x≤0),然后利用两点法画出函数图象即可;
(2)将函数解析式变形为:y=(x﹣2)+2,从而可知直线经过点(2,2);
(3)首先由勾股定理求得OC的长,然后根据三角形的面积为2,可求得OD的长度,从而可得到点D的坐标,将点D的坐标代入函数解析式可求得m的值.
试题解析:解:(1)当x≥0时,y=|x|=x,即y=x(x≥0),将x=0代入得:y=0;将x=1代入得:y=1,
当x≤0时,y=|x|=﹣x,即y=﹣x(x≤0),将x=0代入得:y=0;将x=﹣1代入得:y=1.
过点O(0,0),A(﹣1,1)作射线OA,过点0(0,0),B(1,1)作射线OB,
函数y=|x|的图象如图所示:
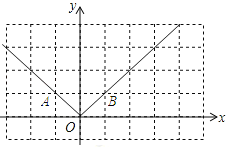
(2)∵y=mx﹣2(m﹣1)=m(x﹣2)+2,
∴x﹣2=0,y=2
∴x=2,y=2,
即函数图象过定点(2,2)…(6分)
(3)如下图:
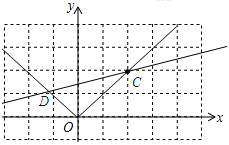
∵函数y=mx﹣2(m﹣1)的图象经过顶点(2,2)
∴OC=![]() =2
=2![]() .
.
∴![]() ODOC=2,
ODOC=2,
∴OD=![]() ,
,
所以点D的坐标为(﹣1,1).
将x=﹣1,y=1代入y=mx﹣2(m﹣1)得:m=![]() .
.


科目:初中数学 来源: 题型:
【题目】学校举办“大爱镇江”征文活动,小明为此次活动设计了一个以三座山为背景的图标(如图),现用红、黄两种颜色对图标中的A、B、C三块三角形区域分别涂色,一块区域只涂一种颜色.
(1)请用树状图列出所有涂色的可能结果;
(2)求这三块三角形区域中所涂颜色是“两块黄色、一块红色”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强学生身体锻炼,某校开展体育“大课间”活动,学校决定在学生中开设A:篮球,B:立定跳远,C:跳绳,D:跑步,E:排球五种活动项目.为了了解学生对五种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两个统计图.请结合图中的信息解答下列问题: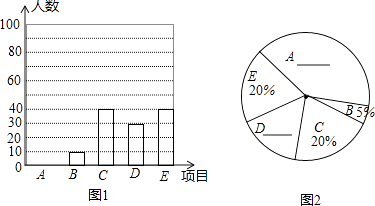
(1)在这项调查中,共调查了名学生;
(2)请将两个统计图补充完整;
(3)若该校有1200名在校学生,请估计喜欢排球的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应区“美丽广西 清洁乡村”的号召,某校开展“美丽广西 清洁校园”的活动,该校经过精心设计,计算出需要绿化的面积为498m2 , 绿化150m2后,为了更快的完成该项绿化工作,将每天的工作量提高为原来的1.2倍.结果一共用20天完成了该项绿化工作.该项绿化工作原计划每天完成多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[感知发现]:如图,是一个“猪手”图,AB∥CD,点E在两平行线之间,连接BE,DE ,我们发现:∠E=∠B+∠D
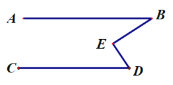
证明如下:过E点作EF∥AB.
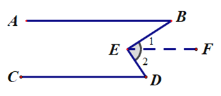
![]() ∠B=∠1(两直线平行,内错角相等.)
∠B=∠1(两直线平行,内错角相等.)
又![]() AB∥CD(已知)
AB∥CD(已知)
![]() CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
![]() ∠2=∠D(两直线平行,内错角相等.)
∠2=∠D(两直线平行,内错角相等.)
![]() ∠1+∠2=∠B+∠D(等式的性质1.)
∠1+∠2=∠B+∠D(等式的性质1.)
即:∠E=∠B+∠D
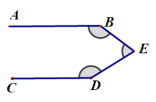
[类比探究]:如图是一个“子弹头”图,AB∥CD,点E在两平行线之间,连接BE,DE.试探究∠E+∠B+∠D=360°.写出证明过程.
[创新应用]:
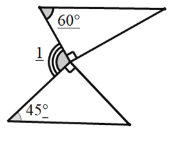
(1).如图一,是两块三角板按如图所示的方式摆放,使直角顶点重合,斜边平行,请直接写出∠1的度数.
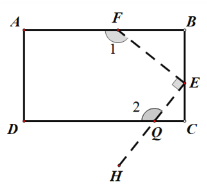
(2).如图二,将一个长方形ABCD按如图的虚线剪下,使∠1=120![]() ,∠FEQ=90°. 请直接写出∠2的度数.
,∠FEQ=90°. 请直接写出∠2的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到![]() .
.

(1)写出由图2所表示的数学等式:________.

(2)写出由图3所表示的数学等式:________.

(3)已知实数![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() .
.
①求![]() 的值.
的值.
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其中部分图象如图所示,下列结论错误的是( )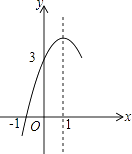
A.4ac<b2
B.方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
C.当y>0时,x的取值范围是﹣1≤x<3
D.当x<0时,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,﹣2),B(6,﹣2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.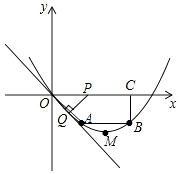
(1)求经过O、A、B三点的抛物线的解析式;
(2)若将△OPQ沿着直线PQ翻折得到△O′PQ,则当t=时,点O′恰好在抛物线上.
(3)在(2)的条件下,记△O′PQ与四边形OABC重叠的面积为S,求S与t的函数关系式,并注明自变量的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com