练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：点D是△ABC中AC的中点，AE∥BC，ED交AB于点G，交BC的延长线于点F．

    （1）求证：△GAE∽△GBF；

    （2）求证：AE=CF；

    （3）若BG：GA=3：1，BC=8，求AE的长．

    【答案】（1）详见解析；（2）详见解析；（3）AE=4

    【解析】

    （1）由AE∥BC可直接判定结论；

    （2）先证△ADE≌△CDF，即可推出结论；

    （3）由△GAE∽△GBF，可用相似三角形的性质求出结果．

    （1）∵AE∥BC，

    ∴△GAE∽△GBF；

    （2）∵AE∥BC，

    ∴∠E=∠F，∠EAD=∠FCD，

    又∵点D是AC的中点，

    ∴AD=CD，

    ∴△ADE≌△CDF(AAS)，

    ∴AE=CF；

    （3）∵△GAE∽△GBF，

    ∴，

    又∵AE=CF，

    ∴3，

    即3，

    ∴AE=4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】山西是我国酿酒最早的地区之一，山西酿酒业迄今为止已有余年的历史.在漫长的历史进程中，山西人民酿造出品种繁多、驰名中外的美酒佳酿，其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒，每瓶成本价是元，经调查发现，当售价为元时，每天可以售出瓶，售价每降低元，可多售出瓶（售价不高于元）

    （1）售价为多少时可以使每天的利润最大？最大利润是多少？

    （2）要使每天的利润不低于元，每瓶竹叶青酒的售价应该控制在什么范围内？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读以下材料，并按要求完成相应的任务．

    “圆材埋壁”是我国古代数学著作《九章算术》中的一个问题：今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？用现在的数学语言表达是：如图，为的直径，弦，垂足为，寸，尺，其中1尺寸，求出直径的长．

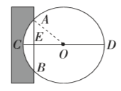
    解题过程如下：

    连接，设寸，则寸．

    ∵尺，∴寸．

    在中，，即，解得，

    ∴寸．

    任务：

    （1）上述解题过程运用了 定理和 定理．

    （2）若原题改为已知寸，尺，请根据上述解题思路，求直径的长．

    （3）若继续往下锯，当锯到时，弦所对圆周角的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=13，BC=15，CA=14，则tan∠EDF的值为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y=ax2-3ax-2交x轴于A、B（A左B右）两点，交y轴于点C，过C作CD∥x轴，交抛物线于点D，E(-2，3)在抛物线上．

    （1）求抛物线的解析式；

    （2）P为第一象限抛物线上一点，过点P作PF⊥CD，垂足为F，连接PE交y轴于G，求证：FG∥DE；

    （3）如图2，在（2）的条件下，过点F作FM⊥PE于M．若∠OFM=45°，求P点坐标．

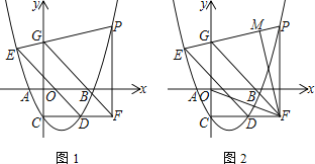
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂加工一批零件，为了提高工人工作积极性，工厂规定每名工人每次薪金如下：生产的零件不超过a件，则每件3元，超过a件，超过部分每件b元，如图是一名工人一天获得薪金y（元）与其生产的件数x（件）之间的函数关系式，则下列结论错误的是（　　）

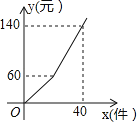
    A.a＝20

    B.b＝4

    C.若工人甲一天获得薪金180元，则他共生产50件

    D.若工人乙一天生产m（件），则他获得薪金4m元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，O是边AC上的点，以OC为半径的圆分别交边BC、AC于点D、E，过点D作DF⊥AB于点F．

    （1）求证：直线DF是⊙O的切线；

    （2）若OC＝1，∠A＝45°，求劣弧DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现

    如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：

    ①的值为　 　；

    ②∠AMB的度数为　 　．

    （2）类比探究

    如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；

    （3）拓展延伸

    在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=，请直接写出当点C与点M重合时AC的长．

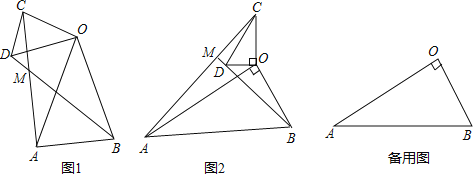
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，下列网格由小正方形组成，点都在正方形网格的格点上.

    （1）在图1中画出一个以线段为边，且与面积相等但不全等的格点三角形；

    （2）在图2和图3中分别画出一个以线段为边，且与相似（但不全等）的格点三角形，并写出所画三角形与的相似比.（相同的相似比算一种）

    （1）

    （2）

    查看答案和解析>>

    同步练习册答案