
【题目】如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣1),△ABC的面积为 ![]() .
.
(1)求该二次函数的关系式;
(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC的外接圆有公共点,求m的取值范围;
(3)在该二次函数的图象上是否存在点D,使四边形ACBD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵OC=1,
∴q=﹣1,
∵△ABC的面积为 ![]() .
.
∴ ![]() OC×AB=
OC×AB= ![]() ,
,
解得AB= ![]() ,
,
设A(a,0),B(b,0),
则a、b是一元二次方程x2+px﹣1=0两个根,
∴a+b=﹣p,ab=﹣1,
∴AB=b﹣a= ![]() =
= ![]() ,
,
解得p= ![]() ,
,
又∵p<0,
∴p= ![]() .
.
所以解析式为:y=x2﹣ ![]() x﹣1;
x﹣1;
(2)
解:如图1所示,
令y=0,
解方程得x2﹣ ![]() x﹣1=0,
x﹣1=0,
得x1=﹣ ![]() ,x2=2,
,x2=2,
所以A( ![]() ,0),B(2,0),
,0),B(2,0),
在直角三角形AOC中可求得AC= ![]() ,同样可求得BC=
,同样可求得BC= ![]() ,
,
显然AC2+BC2=AB2,得三角形ABC是直角三角形.AB为斜边,
所以外接圆的直径为AB= ![]() ,
,
所以 ![]() .
.

(3)
存在,AC⊥BC,
如图2所示,
①若以AC为底边,则BD∥AC,易求AC的解析式为y=﹣2x﹣1,
可设BD的解析式为y=﹣2x+b,
把B(2,0)代入得BD解析式为y=﹣2x+4,
解方程组 
得D( ![]() ,9)
,9)
②若以BC为底边,则BC∥AD,易求BC的解析式为y=0.5x﹣1,
可设AD的解析式为y=0.5x+b,把A( ![]() ,0)代入
,0)代入
得AD解析式为y=0.5x+0.25,
解方程组 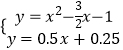
得D( ![]() )
)
综上,所以存在两点:( ![]() ,9)或(
,9)或( ![]() ).
).

【解析】(1)由△ABC的面积为 ![]() ,可得AB×OC=
,可得AB×OC= ![]() ,又二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣1)可求得该二次函数的关系式;(2)根据直线与圆的位置的位置关系确定m的取值范围.(3)四边形ABCD为直角梯形,要分类讨论,即究竟那条边为底.可以分别以AC、BC为底进行讨论.
,又二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣1)可求得该二次函数的关系式;(2)根据直线与圆的位置的位置关系确定m的取值范围.(3)四边形ABCD为直角梯形,要分类讨论,即究竟那条边为底.可以分别以AC、BC为底进行讨论.
【考点精析】解答此题的关键在于理解三角形的外接圆与外心的相关知识,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km. 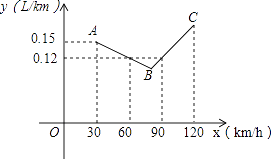
(1)当速度为50km/h、100km/h时,该汽车的耗油量分别为L/km、 L/km.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低?最低是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x﹣
x﹣ ![]() 与x,y轴分别交于点A,B,与反比例函数y=
与x,y轴分别交于点A,B,与反比例函数y= ![]() (k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E. 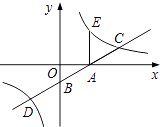
(1)求点A的坐标.
(2)若AE=AC. ①求k的值.
②试判断点E与点D是否关于原点O成中心对称?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y= ![]() x+1与x轴交于点A,且与双曲线y=
x+1与x轴交于点A,且与双曲线y= ![]() 的一个交点为B(
的一个交点为B( ![]() ,m).
,m).
(1)求点A的坐标和双曲线y= ![]() 的表达式;
的表达式;
(2)若BC∥y轴,且点C到直线y= ![]() x+1的距离为2,求点C的纵坐标.
x+1的距离为2,求点C的纵坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )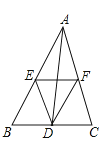
A.DE=DF
B.EF=![]() ?AB
?AB
C.S△ABD=S△ACD
D.AD平分∠BAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,码头A在码头B的正东方向,两个码头之间的距离为32海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.(![]() ≈1.732,结果精确到0.01海里)
≈1.732,结果精确到0.01海里)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com