
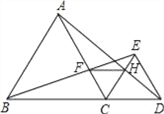
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F, AD交CE于H.
(1)求证:∠CAD=∠CBE
(2)求证:FH∥BD.
【答案】(1)详见解析;(2)详见解析.
【解析】分析:(1)根据等边三角形的性质就可以得出AC=BC,DC=EC,∠ACB=∠DCE=60°,由SAS就可以得出△BCE≌△ACD,从而得出∠CAD=∠CBE;(2)FH与BD平行,由两边相等且一角为60°的三角形为等边三角形得到三角形FCH为等边三角形,利用等边三角形的性质得到一对内错角相等,利用内错角相等两直线平行即可得证.
证明:(1)∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴在△BCE和△ACD中,∵ ,∴△BCE≌△ACD (SAS).
∴∠CAD=∠CBE
(2)由(1)知△BCE≌△ACD,则∠CBF=∠CAH,BC=AC
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上,
∴∠ACH=180°﹣∠ACB﹣∠HCD=60°=∠BCF,
在△BCF和△ACH中,∵ ,∴△BCF≌△ACH (ASA),∴CF=CH,
又∵∠FCH=60°,∴△CHF为等边三角形∴∠FHC=∠HCD=60°,∴FH∥BD.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】问题背景
如图![]() ,在正方形
,在正方形![]() 的内部,作
的内部,作![]() ,根据三角形全等的条件,易得
,根据三角形全等的条件,易得![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,从而得到四边形
,从而得到四边形![]() 是正方形.
是正方形.
类比探究
如图![]() ,在正
,在正![]() 的内部,作
的内部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两相交于
两两相交于![]() ,
, ![]() ,
, ![]() 三点(
三点(![]() ,
, ![]() ,
, ![]() 三点不重合).
三点不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(![]() )
)![]() 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
(![]() )进一步探究发现,图
)进一步探究发现,图![]() 中的
中的![]() 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设![]() ,
, ![]() ,
, ![]() ,请探索
,请探索![]() ,
, ![]() ,
, ![]() 满足的等量关系.
满足的等量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知到直线l的距离等于a的所有点的集合是与直线l平行且距离为a的两条直线l1、l2(如图①).
(1)在图②的平面直角坐标系中,画出到直线y=x+2![]() 的距离为1的所有点的集合的图形.并写出该图形与y轴交点的坐标.
的距离为1的所有点的集合的图形.并写出该图形与y轴交点的坐标.
(2)试探讨在以坐标原点O为圆心,r为半径的圆上,到直线y= x + 2![]() 的距离为1的点的个数与r的关系.
的距离为1的点的个数与r的关系.
(3)如图③,若以坐标原点O为圆心,2为半径的圆上只有两个点到直线y= x + b的距离为1,则b的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 在同一平面内,过一点有且只有一条直线与已知直线垂直
B. 对顶角相等
C. 两直线平行,同位角相等
D. 同旁内角互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
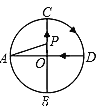
【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是 ( )
A.  B.
B. 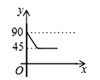 C.
C. 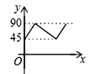 D.
D. 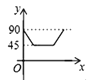
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com