
【题目】已知反比例函数y=(2m﹣1)xm2﹣2 , 当x>0时,y随着x的增大而减小.
(1)求m的值;
(2)当1<x<4时,求y的取值范围.
【答案】解:(1)∵反比例函数y=(2m﹣1)xm2﹣2 , 当x>0时,y随着x的增大而减小,
∴m2﹣2=﹣1,2m﹣1>0,
解得:m=±1,m>![]() ,
,
故m=1;
(2)∵y=x﹣1 ,
∴当x=1时,y=1,x=4时,y=![]() ,
,
∴当1<x<4时,y的取值范围是:![]() <y<1.
<y<1.
【解析】(1)利用反比例函数的定义以及其性质得出m的值即可;
(2)分别将x=1,x=4代入求出对应y的值,即可得出答案.
【考点精析】本题主要考查了反比例函数的概念的相关知识点,需要掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数才能正确解答此题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】据中国电子商务研究中心监测数据显示,2015年第一季度中国轻纺城市场群的商品成交额达27 800 000 000元,将27 800 000 000用科学记数法表示为( )
A.2.78×1010
B.2.78×1011
C.27.8×1010
D.0.278×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第四届长春图书博览会在长春国际会展中心开幕,来白全国各地百余家出版单位的350000种出版物登场.350000这个数用科学记数法可以表示为( )
A.35×101B.0.35×106C.3.5×106D.3.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B= . 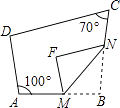
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年政府工作报告中指出,5年来我国有约80000000农业转移人口成为城镇居民.用科学记数法表示数据80000000,其结果是( )
A.80×106B.0.8×108C.8×107D.8×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表).
月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |

设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
t≤150 | 150<t<350 | t=350 | t>350 | |
方式一计费/元 | 58 | 108 | ||
方式二计费/元 | 88 | 88 | 88 |
(2)当t为何值时,两种计费方式的费用相等?
(3)当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com