
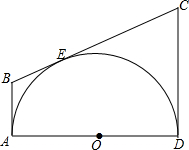
 如图所示,AD为半圆O的直径,AB,CD与半圆O相切于A,D两点,BC与半圆O相切于点E.若AB=4,CD=9,则半圆O的直径是多少?
如图所示,AD为半圆O的直径,AB,CD与半圆O相切于A,D两点,BC与半圆O相切于点E.若AB=4,CD=9,则半圆O的直径是多少? 分析 根据AB,CD与半圆O相切于A,D两点,于是得到∠BAD=90°,∠ADC=90°,又BC与圆O相切于点E,且AB=4,CD=9,求得BE=AB=4,CE=CD=9,于是得到BC=BE+EC=13,过B作BF⊥DC于F点,则四边形ABFD为矩形,根据矩形的性质得到AB=DF=4,求出FC=5,在Rt△CFB中,根据勾股定理得到BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=12,即可得到结论.
解答  解:∵AB,CD与半圆O相切于A,D两点,∴∠BAD=90°,
解:∵AB,CD与半圆O相切于A,D两点,∴∠BAD=90°,
∴∠ADC=90°,
又BC与圆O相切于点E,且AB=4,CD=9,
∴BE=AB=4,CE=CD=9,
∴BC=BE+EC=13,
过B作BF⊥DC于F点,则四边形ABFD为矩形,
∴AB=DF=4,
∴FC=5,
在Rt△CFB中,根据勾股定理得:BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=12,
∴AD=BF=12.
∴半圆O的直径是12.
点评 此题考查了切线的判定与性质,切线长定理,勾股定理,梯形的面积公式,以及矩形的判定与性质,熟练掌握定理及性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
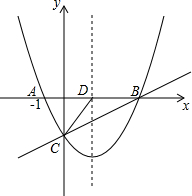 如图,抛物线y=$\frac{1}{2}$x2+nx-2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+nx-2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
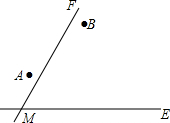 两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com