
 ��ͼ��������y=$\frac{1}{2}$x2+nx-2��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0����
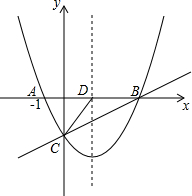
��ͼ��������y=$\frac{1}{2}$x2+nx-2��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0�������� ��1������A���������߽���ʽ���ɵ�n��ֵ���̶��ɵ������ߵı���ʽ��
��2����ΪP�������߶Գ����ϣ���ɷ�����������ۣ��١�CPD=90�㣬�ڡ�PCD=90�㣬�ֱ������P���꼴�ɣ�
��3����ȷ��ֱ��BC����ʽ�������M���꣬�̶��ó���N�����ʾ��MN�ij��ȣ�����S�ı���CDBN=S��CDB+S��BMN+S��CMN����϶��κ�������ֵ������ȷ����M�����꼰��������
��� �⣺��1���ѵ�A��-1��0������y=$\frac{1}{2}$x2+nx-2�ã�n=-$\frac{3}{2}$��
�������ߵı���ʽΪ��y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
��2�����ڣ�
��y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
�������߶Գ���Ϊ��x=$\frac{3}{2}$��
�ٵ���CPD=90��ʱ������Ȼ��P����Ϊ��$\frac{3}{2}$��-2����
�ڵ���PCD=90��ʱ����ͼ����ʾ��
CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=$\frac{5}{2}$��
��cos��CDP=$\frac{CD}{PD}$=cos��DCO=$\frac{OC}{CD}$=$\frac{4}{5}$��
��PD=$\frac{25}{8}$��
���P������$\frac{3}{2}$��-$\frac{25}{8}$����
���Ͽɵã����ڵ�P��ʹ��PCD��ֱ�������Σ���P����Ϊ��$\frac{3}{2}$��-2����$\frac{3}{2}$��-$\frac{25}{8}$����
��3�����߶�BC��һ��M��MN��x�ᣬ����ΪF���������߽��ڵ�N������C��CE��MN������ΪE����ͼ����ʾ��
�ɶ��κ�������ʽ�ɵõ�B��4��0������C��0��-2����
��BC����ʽΪy=kx+b��
��$\left\{\begin{array}{l}{4k+b=0}\\{b=-2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$��
��ֱ��BC����ʽΪy=$\frac{1}{2}$x-2��
���M��������m��$\frac{1}{2}$m-2�������N��������m��$\frac{1}{2}$m2-$\frac{3}{2}$m-2����
MN=��$\frac{1}{2}$m-2��-��$\frac{1}{2}$m2-$\frac{3}{2}$m-2��=-$\frac{1}{2}$m2+2m��
��S�ı���CDBN=S��CDB+S��BMN+S��CMN
=$\frac{1}{2}$BD��OC+$\frac{1}{2}$MN��BF+$\frac{1}{2}$MN��CE
=$\frac{1}{2}$��4-$\frac{3}{2}$����2+$\frac{1}{2}$MN��BF+CE��
=$\frac{5}{2}$+$\frac{1}{2}$��-$\frac{1}{2}$m2+2m����4
=-m2+4m+$\frac{5}{2}$
=-��m-2��2+$\frac{13}{2}$��
��m=2ʱ��S�ı���CDBN�����ֵ�����ֵΪ$\frac{13}{2}$����ʱ��M������Ϊ��2��-1����
���� ���⿼���˶��κ������ۺϣ��漰�˴���ϵ��������κ�������ʽ�����κ�������ֵ�������ε�����������Ĺؼ������ν��˼�뼰��������˼������ã��ѶȽϴ�


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
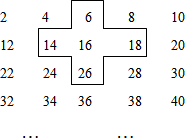 ̽�����ɽ�������ż2��4��6��8�������ų������
̽�����ɽ�������ż2��4��6��8�������ų�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
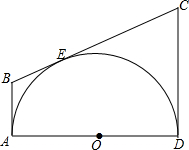 ��ͼ��ʾ��ADΪ��ԲO��ֱ����AB��CD���ԲO������A��D���㣬BC���ԲO�����ڵ�E����AB=4��CD=9�����ԲO��ֱ���Ƕ��٣�
��ͼ��ʾ��ADΪ��ԲO��ֱ����AB��CD���ԲO������A��D���㣬BC���ԲO�����ڵ�E����AB=4��CD=9�����ԲO��ֱ���Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
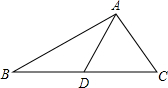 ��ABC�У�ADΪBC���ϵ����ߣ���֪AB=5��AC=3�����߶�AD�ij���ȡֵ��Χ��
��ABC�У�ADΪBC���ϵ����ߣ���֪AB=5��AC=3�����߶�AD�ij���ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
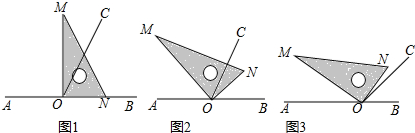
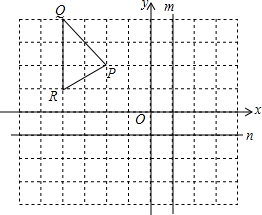 ��ͼ��ÿ�������εı߳�����1���ֱ�������PQR����ֱ��x=1����Ϊm����ֱ��y=-1����Ϊn���ԳƵ�ͼ�Σ����ǵĶ�Ӧ�������֮��ֱ���ʲô��ϵ��
��ͼ��ÿ�������εı߳�����1���ֱ�������PQR����ֱ��x=1����Ϊm����ֱ��y=-1����Ϊn���ԳƵ�ͼ�Σ����ǵĶ�Ӧ�������֮��ֱ���ʲô��ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
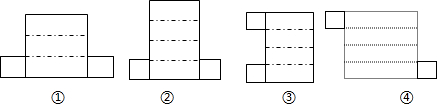
| A�� | �٢� | B�� | �٢� | C�� | �٢� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com