
分析 (1)根据0指数幂及负整数指数幂的计算法则、数的乘方法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:(1)原式=-1+$\frac{1}{2}$-1+2
=$\frac{1}{2}$;
(2)原式=$\frac{2(x+1)+(x-1)}{(x+1)(x-1)}$•(x2-1)
=2x+2+x-1
=3x+1,
解方程x2-4x+3=0得,(x-1)(x-3)=0,
x1=1,x2=3.
当x=1时,原式无意义;
当x=3时,原式=3×3+1=10.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:填空题
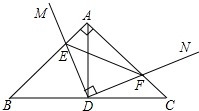 如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10.
如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
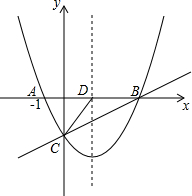 如图,抛物线y=$\frac{1}{2}$x2+nx-2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+nx-2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
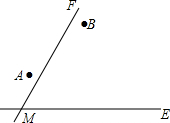 两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com