Question

在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4．则下列四个结论：①AE∥BC；②∠ADE=∠BDC；③△BDE是等边三角形；④△ADE的周长是9．其中正确的结论是 （把你认为正确结论的序号都填上）．

 

 

Answer 1

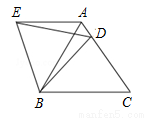
①③④．

【解析】

试题分析：∵△ABC是等边三角形，∴∠ABC=∠C=60°，

∵将△BCD绕点B逆时针旋转60°，得到△BAE，∴∠EAB=∠C=∠ABC=60°，

∴AE∥BC，故选项①正确；

∵△ABC是等边三角形，∴AC=AB=BC=5，

∵△BAE△BCD逆时针旋旋转60°得出，∴AE=CD，BD=BE，∠EBD=60°，∴AE+AD=AD+CD=AC=5，

∵∠EBD=60°，BE=BD，∴△BDE是等边三角形，故选项③正确；

∴DE=BD=4，∴△AED的周长=AE+AD+DE=AC+BD=9，故选项④正确；

而②没有条件证明∠ADE=∠BDC，∴结论错误的是②，

故答案为：①③④．

考点：1．旋转的性质；2．平行线的判定；3．等边三角形的性质．