练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    顺次连接矩形四边的中点所得的四边形是                   （▲）
    A．等腰梯形B．矩形C．平行四边形D．菱形
    D
    如图，E、F、G、H分别为矩形ABCD四边的中点．
    求证：四边形EFGH为菱形．
    证明：连接AC、BD，在△ABD中，
    ∵AH=HD，AE=EB∴EH=12BD，同理FG=12BD，HG=12AC，EF=12AC，
    又∵在矩形ABCD中，AC=BD，∴EH=HG=GF=FE，∴四边形EFGH为菱形．故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图，在直角坐标系中，是原点，三点的坐标分别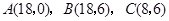
    ，四边形是梯形，点同时从原点出发，分别作匀速运动，其中点沿向终点运动，速度为每秒个单位，点沿向终点运动，当这两点有一点到达自己的终点时，另一点也停止运动．
    小题1:求直线的解析式．
    小题2:设从出发起，运动了秒．如果点的速度为每秒个单位，试写出点的坐标，并写出此时 的取值范围．
    小题3:设从出发起，运动了秒．当，两点运动的路程之和恰好等于梯形的周长的一半，这时，直线能否把梯形的面积也分成相等的两部分，如有可能，请求出的值；如不可能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，是的一条角平分线，∥交于点，∥交于点，求证：四边形是菱形（7分）

    证明：是的一条角平分线

    ∥
    （                               ）
    ____________（等量代换）
    ____________(等角对等边)
    又∥，∥
    即___________________,_____________________
    四边形是平行四边形（_________________________________）
    是菱形（____________________________________________）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，分别是□ABCD的对角线上的两点，且，求证：

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    有若干张如图所示的正方形和长方形卡片，如果要拼一个长为（2a+b），宽为（a+b）的矩形，则需要A类卡片               张，B类卡片              张，C类卡片               张，请你在右下角的大矩形中画出一种拼法。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （本题满分7分）
    如图所示，在平行四边形的各边上，分别取点
    ，使．
    求证：四边形为平行四边形．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

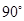    （本小题满分6分）如图，在梯形ABCD中，AD∥BC，∠B ＝，∠C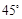＝，AD＝1，BC＝4，点E为AB中点，EF∥DC交BC于点F，求EF的长。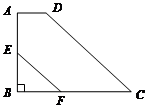

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （本题满分10分）如图，在梯形中，两点在边上，且四边形是平行四边形．

    （1）与有何等量关系？请说明理由；
    （2）当时，求证：是矩形．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    等腰梯形的一个内角为1200，上底为10，下底为30，则它的腰长为 （       ）
    A．10B．20C．D．

    查看答案和解析>>

    同步练习册答案