
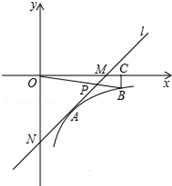
 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,
如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,分析 (1)设直线l的解析式为y=kx+b,利用待定系数法即可求得直线的解析式;根据已知求得A点的坐标,然后把A代入y=$\frac{k}{x}$(x>0)即可求得解析式;
(2)根据反比例函数系数k的几何意义得出S△OBC=$\frac{1}{2}$|k|=$\frac{3}{2}$,进而得出S△ONP=3×$\frac{3}{2}$=$\frac{9}{2}$,设P点的坐标为(a,b)(a>0),根据S△ONP=$\frac{1}{2}$ON•xP=$\frac{1}{2}$×4×a=$\frac{9}{2}$,即可求得a的值,进而求得P的坐标.
解答 解:(1)设直线l的解析式为y=kx+b,
∵直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),
∴$\left\{\begin{array}{l}{3k+b=0}\\{b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-4}\end{array}\right.$
∴直线l的解析式y=$\frac{4}{3}$x-4,
∵A点是线段MN的中点,
∴A点的坐标($\frac{3}{2}$,-2),
代入y=$\frac{k}{x}$(x>0)求得,k=-3,
∴反比例函数的解析式为y=-$\frac{3}{x}$.
(2)∵S△OBC=$\frac{1}{2}$|k|=$\frac{3}{2}$,△ONP的面积是△OBC面积的3倍,
∴S△ONP=3×$\frac{3}{2}$=$\frac{9}{2}$
∵N(0,-4),
∴ON=4,
设P点的坐标为(a,b)(a>0),
∴S△ONP=$\frac{1}{2}$×4×a=$\frac{9}{2}$,
∴a=$\frac{9}{4}$,
∴b=$\frac{4}{3}$×$\frac{9}{4}$-4=-1,
∴P($\frac{9}{4}$,-1).
点评 本题考查了用待定系数法求一次函数和反比例函数的解析式,三角形面积,一次函数与反比例函数的交点问题的应用.此题难度适中,注意掌握数形结合思想与方程思想的应用.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:选择题
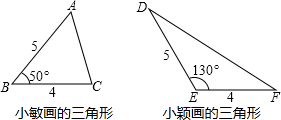
| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | C. | S△ABC=S△DEF | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10个 | B. | 15个 | C. | 20个 | D. | 25个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
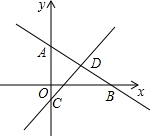 如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=$\frac{5}{6}x$-1交于点D,C为直线y轴的交点.
如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=$\frac{5}{6}x$-1交于点D,C为直线y轴的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
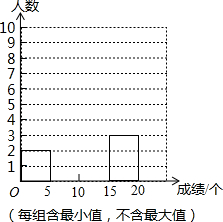 某校为了解九年级300名男生的体能情况,随机抽取了部分九年级男生进行“引体向上”测试,这些男生的测试成绩(单位:个)如下:
某校为了解九年级300名男生的体能情况,随机抽取了部分九年级男生进行“引体向上”测试,这些男生的测试成绩(单位:个)如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
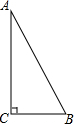 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
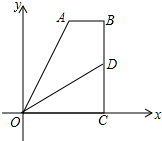 已知如图,在平面直角坐标系中,四边形ABCD的顶点A,B在第一象限,AB∥x轴,∠B=90°,AB+OC=OA,OD平分∠AOC交BC于点D.若四边形ABDO的面积为4,反比例函数y=$\frac{k}{x}$的图象经过点D,点A,则k的值是( )
已知如图,在平面直角坐标系中,四边形ABCD的顶点A,B在第一象限,AB∥x轴,∠B=90°,AB+OC=OA,OD平分∠AOC交BC于点D.若四边形ABDO的面积为4,反比例函数y=$\frac{k}{x}$的图象经过点D,点A,则k的值是( )| A. | 8 | B. | 6 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com