
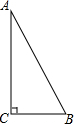
 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.分析 (1)只需按照题目的要求画图即可;
(2)①过点O作OD⊥AB,垂足为D,如图所示,只需证明OD=OC即可;②在Rt△OBC中,运用三角函数可求出$\frac{OC}{BC}$=$\frac{2}{3}$,从而得到$\frac{OD}{BC}$=$\frac{OC}{BC}$=$\frac{2}{3}$,易证Rt△ADO∽Rt△ACB,运用相似三角形的性质可求得AD=8,然后在Rt△ADO中运用勾股定理即可解决问题.
解答 解:(1)如图,⊙O即为所求作;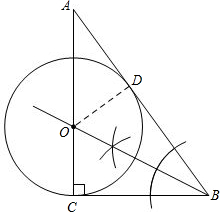
(2)AB与⊙O相切,理由如下:
过点O作OD⊥AB,垂足为D,如图所示.
∵∠ACB=90°,∴OC⊥BC.
∵BO是∠ABC的平分线,OD⊥AB,OC⊥BC,
∴OC=OD.
∴AB与⊙O相切;
(3)在Rt△OBC中,
tan∠OBC=$\frac{OC}{BC}$=$\frac{2}{3}$,
∴$\frac{OD}{BC}$=$\frac{OC}{BC}$=$\frac{2}{3}$.
又∵∠ADO=∠ACB=90°,∠A=∠A,
∴Rt△ADO∽Rt△ACB,
∴$\frac{AD}{AC}$=$\frac{OD}{BC}$=$\frac{2}{3}$,
∴AD=$\frac{2}{3}$AC=$\frac{2}{3}$×12=8.
设⊙O的半径为r,则OD=OC=r,AO=12-r.
在Rt△ADO中,
根据勾股定理可得r2+82=(12-r)2,
解得r=$\frac{10}{3}$,
∴⊙O的半径是$\frac{10}{3}$.
点评 本题是一道操作探究题,考查了切线的判定、角平分线的性质、三角函数、相似三角形的判定与性质、勾股定理等知识,注重对动手能力、推理能力、运算能力的考查,是一道好题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
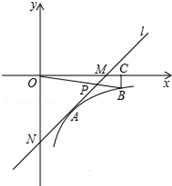 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,
如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
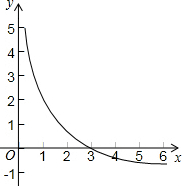 小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )
小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,立即按原路返回,返回时的速度是去时速度的2倍,结果与慢车同时回到甲地.慢车距出发地的路程y1(千米)与出发后所用的时间x(小时)的关系如图所示.
快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,立即按原路返回,返回时的速度是去时速度的2倍,结果与慢车同时回到甲地.慢车距出发地的路程y1(千米)与出发后所用的时间x(小时)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com